Critère diagonalisabilité
96 messages
- Page 5 sur 5 - 1, 2, 3, 4, 5
@ilikoko : OK, je comprends. Dans mon esprit le cas a=b était déjà traité. Tu l'avais fait en tout cas pour n=3, et je t'avais signalé que ça marchait pour tout n.
Bon, Kolis, l'a refait.
(
C'est une fantaisie du compilateur LaTeX de ce forum. Ca m'a aussi surpris la première fois que je m'en suis aperçu. Il suffit de laisser une espace devant le signe - pour que tout rentre dans l'ordre.
Bon, Kolis, l'a refait.
(
Kolis a écrit:..... il y a un bug : j'ai écrit "valeur propre -a " et je vois apparaître f(x)=x^2...
C'est une fantaisie du compilateur LaTeX de ce forum. Ca m'a aussi surpris la première fois que je m'en suis aperçu. Il suffit de laisser une espace devant le signe - pour que tout rentre dans l'ordre.
Merci pour le tuyau et bonne nuit !
entretemps j'ai trouvé plus rapide pour le cas (c'est peut-être déjà dit et je m'excuse de ne pas l'avoir lu !). La matrice
(c'est peut-être déjà dit et je m'excuse de ne pas l'avoir lu !). La matrice  est alors
est alors ) où
où 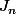 est la matrice où tous les coefficients valent 1. Comme
est la matrice où tous les coefficients valent 1. Comme  on dispose d'un polynôme annulateur de degré 2 pour
on dispose d'un polynôme annulateur de degré 2 pour  avec des racines distinctes si
avec des racines distinctes si 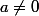 .
.
entretemps j'ai trouvé plus rapide pour le cas
L'égalité  se montre facilement sans récurrence en remarquant que la dérivée de la
se montre facilement sans récurrence en remarquant que la dérivée de la  -ème colonne de
-ème colonne de  est le
est le  -ème vecteur de la base canonique et que le cofacteur d'indice
-ème vecteur de la base canonique et que le cofacteur d'indice ) est tout bêtement le déterminant de
est tout bêtement le déterminant de  .
.
Si tu as déjà démontré que et
et 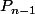 n'ont pas de racine commune, tu déduis de
n'ont pas de racine commune, tu déduis de  que toutes les racines de
que toutes les racines de  sont simples, et donc ...
sont simples, et donc ...
Si tu as déjà démontré que
Robot a écrit:L'égalitése montre facilement sans récurrence en remarquant que la dérivée de la
-ème colonne de
est le
-ème vecteur de la base canonique et que le cofacteur d'indice
est tout bêtement le déterminant de
.
J ai compris ça mais le reste non
Pourquoi on n ecrit pas directement apres ça Pn'=nP(n-1)
Et je ne comprends pas pourquoi si on a Pn'=nP(n-1) et ( pn et pn-1 n ont pas de racines communs ) alors pn est scindé à racine simple
anouai a écrit:J ai compris ça mais le reste non
Pourquoi on n ecrit pas directement apres ça Pn'=nP(n-1)
Et je ne comprends pas pourquoi si on a Pn'=nP(n-1) et ( pn et pn-1 n ont pas de racines communs ) alors pn est scindé à racine simple
Moi, je ne comprends rien à tes questions. Sauf la dernière question, pour laquelle je te renvoie à ton cours : racine multiple de P = racine commune de P et P'.
Robot a écrit:Moi, je ne comprends rien à tes questions. Sauf la dernière question, pour laquelle je te renvoie à ton cours : racine multiple de P = racine commune de P et P'.
Ça existe dans le programme des classes preparatoir filliere mp?
Je ne me rappelle pas qu on a fait ça dans le classe avec le prof
96 messages
- Page 5 sur 5 - 1, 2, 3, 4, 5
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 9 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
