Critère diagonalisabilité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Robot
 par Robot » 07 Nov 2015, 22:43
par Robot » 07 Nov 2015, 22:43
ilikoko123 a écrit: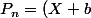P_{n-1} + (a+X)(a-b)P_{n-2}-a(a+X)(b+X)^{n-2})
??
:triste:
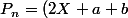P_{n-1}-(X+a)(X+b)P_{n-2})
Avec ça on peut voir sous les hypothèses
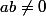
et
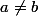
que

et
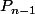
n'ont pas de racine commune, et donc que

n'a que des racines simples.
Maintenant, l'autre méthode est très astucieuse. Si tu l'as trouvée toi-même, félicitations !
-
ilikoko123
- Membre Relatif
- Messages: 219
- Enregistré le: 09 Oct 2015, 21:40
-
 par ilikoko123 » 08 Nov 2015, 00:16
par ilikoko123 » 08 Nov 2015, 00:16
j'ignore ce qui ne va pas avec mes determinants :(
en tout cas merci pour l'aide et pour la longue discussion je vous suis reconnaissant :D
-
ilikoko123
- Membre Relatif
- Messages: 219
- Enregistré le: 09 Oct 2015, 21:40
-
 par ilikoko123 » 08 Nov 2015, 00:47
par ilikoko123 » 08 Nov 2015, 00:47
remarquez que ce topic a atteint le top des nombres d'affichages :D
-
anouai
- Membre Naturel
- Messages: 18
- Enregistré le: 06 Nov 2015, 12:26
-
 par anouai » 08 Nov 2015, 08:52
par anouai » 08 Nov 2015, 08:52
Moi je comprends pas ce que vous avez dit robot
P_n=(2X+a+b)P_{n-1}-(X+a)(X+b)P_{n-2} et ab\neq 0 et a\neq b => P_n et P_{n-1} n'ont pas de racine commune => P_n n'a que des racines simples
D'où vient ces implications
Je n ai compris nî la 1er ni la 2em implication
-
anouai
- Membre Naturel
- Messages: 18
- Enregistré le: 06 Nov 2015, 12:26
-
 par anouai » 08 Nov 2015, 09:01
par anouai » 08 Nov 2015, 09:01
Pour la 2eme méthode
J ai calculé det(M+xU) j ai trouvé
det(M+xU)=cx+d (avec c et d dependent de n)
Ce det ne donne acune condition sur la diagonalisation de M ?!
-
Robot
 par Robot » 08 Nov 2015, 10:10
par Robot » 08 Nov 2015, 10:10
ilikoko123 a écrit:j'ignore ce qui ne va pas avec mes determinants

en tout cas merci pour l'aide et pour la longue discussion je vous suis reconnaissant

L'obtention de la relation de récurrence est pourtant très simple. On part de la matrice
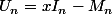
. On soustrait la deuxième ligne de la première puis la deuxième colonne de la première. La première ligne a ses deux premiers coefficients

et
)
les autres sont nuls. On développe le déterminant suivant la première ligne. On a d'une part
)
fois le déterminant de
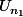
, d'autre part

fois le déterminant d'une matrice dont la première colonne a pour premier coefficient
)
et tous les autres coefficients nuls. Ce dernier déterminant est donc
)
fois le déterminant de
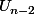
. En remettant tout ensemble,
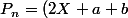P_{n-1}-(X+a)(X+b)P_{n-2})
pour

. Pour les deux premiers,
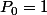
et
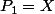
.
Pour conclure, sous l'hypothèse
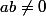
et
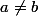
:
1°) Montrer que
\neq 0)
et
\neq 0)
. (Indication : pour

,
 = (b-a)P_{n-1}(-a))
.)
2°) Montrer que, pour

, si

est racine de

et
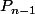
, alors

est aussi racine de
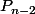
. En déduire que

et
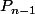
n'ont pas de racine commune.
3°) Montrer que

et en déduire que
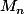
est diagonalisable sur

.
-
anouai
- Membre Naturel
- Messages: 18
- Enregistré le: 06 Nov 2015, 12:26
-
 par anouai » 08 Nov 2015, 12:06
par anouai » 08 Nov 2015, 12:06
La première question on la montre pas une récurence
C est facile
Pour La deuxième question
pour n>1 si c est racine de P_n et P_{n-1}, alors P_n(c)=(2c+a+b)P_{n-1}(c)-(c+a)(c+b)P_{n-2}(c) alors P_{n-2}(c)=0
Mais comment peut on déduire que P_n et P_{n-1} n'ont pas de racine commune.
-
ilikoko123
- Membre Relatif
- Messages: 219
- Enregistré le: 09 Oct 2015, 21:40
-
 par ilikoko123 » 08 Nov 2015, 12:07
par ilikoko123 » 08 Nov 2015, 12:07
parfait :) pourtant j'aimerais allonger cette discussion en disant que ce n'est qu'une condition suffisante
-
ilikoko123
- Membre Relatif
- Messages: 219
- Enregistré le: 09 Oct 2015, 21:40
-
 par ilikoko123 » 08 Nov 2015, 12:10
par ilikoko123 » 08 Nov 2015, 12:10
Robot a écrit:L'obtention de la relation de récurrence est pourtant très simple. On part de la matrice
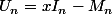
. On soustrait la deuxième ligne de la première puis la deuxième colonne de la première. La première ligne a ses deux premiers coefficients

et
)
les autres sont nuls. On développe le déterminant suivant la première ligne. On a d'une part
)
fois le déterminant de
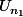
, d'autre part

fois le déterminant d'une matrice dont la première colonne a pour premier coefficient
)
et tous les autres coefficients nuls. Ce dernier déterminant est donc
)
fois le déterminant de
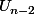
. En remettant tout ensemble,
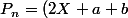P_{n-1}-(X+a)(X+b)P_{n-2})
pour

. Pour les deux premiers,
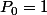
et
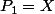
.
Pour conclure, sous l'hypothèse
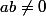
et
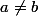
:
1°) Montrer que
\neq 0)
et
\neq 0)
. (Indication : pour

,
 = (b-a)P_{n-1}(-a))
.)
2°) Montrer que, pour

, si

est racine de

et
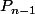
, alors

est aussi racine de
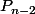
. En déduire que

et
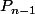
n'ont pas de racine commune.
3°) Montrer que

et en déduire que
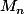
est diagonalisable sur

.
Parfait

pourtant il me parait que toutes les méthodes ne montrent qu'une condition suffisante :p
-
ilikoko123
- Membre Relatif
- Messages: 219
- Enregistré le: 09 Oct 2015, 21:40
-
 par ilikoko123 » 08 Nov 2015, 12:15
par ilikoko123 » 08 Nov 2015, 12:15
anouai a écrit:La première question on la montre pas une récurence
C est facile
Pour La deuxième question
pour n\geq 2, si c est racine de P_n et P_{n-1}, alors P_n(c)=(2c+a+b)P_{n-1}(c)-(c+a)(c+b)P_{n-2}(c) alors P_{n-2}(c)=0
Mais comment peut on déduire que P_n et P_{n-1} n'ont pas de racine commune.
Recurence ,, Pn et Pn-1 n'ont pas de racines communes implique que Pn+1 et Pn n'ont pas de racines communes , sinon Pn-1 aura aussi cette racine commune selon la question precedente mais l'heredite assure que Pn et Pn-1 n'ont pas de racines communes ..!

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 08 Nov 2015, 12:55
par Lostounet » 08 Nov 2015, 12:55
Bonjour,
Robot a écrit:Maintenant, l'autre méthode est très astucieuse. Si tu l'as trouvée toi-même, félicitations !
A vrai dire je ne comprends pas comment ils dénombrent le nombre de termes nuls/non nuls dans les 2^n termes dans ce corrigé que j'ai trouvé sur le net:

2^n termes ok car chaque colonne va donner 2 déterminants à chaque fois. Et les (n + 1) termes non nuls alors? Pour moi c'est plutot n. Quelqu'un pourrait-il m'expliquer?
Et pour tes 3 questions Robot, je réfléchis.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
ilikoko123
- Membre Relatif
- Messages: 219
- Enregistré le: 09 Oct 2015, 21:40
-
 par ilikoko123 » 08 Nov 2015, 13:22
par ilikoko123 » 08 Nov 2015, 13:22
Tu préfère te diriger vers exo7 et négliger nos post pour des raisons que j'ignore, tu pourrait demander tout simplement pourquoi la fonction est affine et la réponse et très simple et DEJA mentionnée dans un post avant sans recourir aux puissances de 2 :p
-
ilikoko123
- Membre Relatif
- Messages: 219
- Enregistré le: 09 Oct 2015, 21:40
-
 par ilikoko123 » 08 Nov 2015, 13:23
par ilikoko123 » 08 Nov 2015, 13:23
Lostounet a écrit:Bonjour,
A vrai dire je ne comprends pas comment ils dénombrent le nombre de termes nuls/non nuls dans les 2^n termes dans ce corrigé que j'ai trouvé sur le net:

2^n termes ok car chaque colonne va donner 2 déterminants à chaque fois. Et les (n + 1) termes non nuls alors? Pour moi c'est plutot n. Quelqu'un pourrait-il m'expliquer?
Et pour tes 3 questions Robot, je réfléchis.
Tu préfère te diriger vers exo7 et négliger nos post pour des raisons que j'ignore, tu pourrait demander tout simplement pourquoi la fonction est affine et la réponse et très simple et DEJA mentionnée dans un post avant sans recourir aux puissances de 2 :p

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 08 Nov 2015, 13:26
par Lostounet » 08 Nov 2015, 13:26
J'ai lu chaque post de la discussion mais je souhaite quand même comprendre si tu pouvais m'expliquer ce passage qui est très en lien avec la méthode que tu proposes (c'est pour cela que je post à la suite). Sans opérations sur les lignes.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
Robot
 par Robot » 08 Nov 2015, 13:40
par Robot » 08 Nov 2015, 13:40
ilikoko123 a écrit:Parfait

pourtant il me parait que toutes les méthodes ne montrent qu'une condition suffisante :p
Que veux-tu dire ? Condition suffisante pour quoi ? Exprime-toi plus clairement.
-
Robot
 par Robot » 08 Nov 2015, 13:49
par Robot » 08 Nov 2015, 13:49
Lostounet a écrit:Bonjour,
2^n termes ok car chaque colonne va donner 2 déterminants à chaque fois. Et les (n + 1) termes non nuls alors? Pour moi c'est plutot n. Quelqu'un pourrait-il m'expliquer?
On utilise la multilinéarité du déterminant (le "linéarité" du corrigé est assez malheureux), disons par rapport aux colonnes, en écrivant chaque colonne comme somme d'une colonne de la matrice de départ et d'une colonne constituée uniquement de

.
Quand on développe, on obtient

déterminants. Tous ceux qui comportent plus d'une colonne de

sont nuls. Ne restent que le déterminant de la matrice de départ, et les

déterminants qui ont chacun une et une seule colonne de

.
-
ilikoko123
- Membre Relatif
- Messages: 219
- Enregistré le: 09 Oct 2015, 21:40
-
 par ilikoko123 » 08 Nov 2015, 13:49
par ilikoko123 » 08 Nov 2015, 13:49
Oué avec plaisir, le determinant est une forme n lineaire et pour mieux comprendre elle peut etre vue d'un coté comme une application n lineaire de l'espace Mn,1 vers R , la variable dedans n'est que les colonnes du determinant qu'on calcule , ces colonnes comme tu peux remarquer peuvent etre la somme de deux collones , l'une des deux ne contient que des x , et puisque le det est n lineaire et apres qu'on decompose chaque collone ainsi ca devient une histoire de denombrement pour trouver combiens de fois on trouver un n uplet ( de colonnes ) ou la colonne en x se repete deux fois
-
ilikoko123
- Membre Relatif
- Messages: 219
- Enregistré le: 09 Oct 2015, 21:40
-
 par ilikoko123 » 08 Nov 2015, 13:52
par ilikoko123 » 08 Nov 2015, 13:52
14:49 avec un decalage de quelques secondes :D
-
ilikoko123
- Membre Relatif
- Messages: 219
- Enregistré le: 09 Oct 2015, 21:40
-
 par ilikoko123 » 08 Nov 2015, 13:55
par ilikoko123 » 08 Nov 2015, 13:55
L'exercice demande une condition suffisante et necessaire sur a rt b pour que la matrice soit diagonalisable , faut montrer que si la matrice est diagonalisable alors ab est non nul et a est different de b , ie : le fait que le polynome caractéristique n'admet que des racines simples n'est pas une condition necessaire
-
Kolis
- Membre Relatif
- Messages: 482
- Enregistré le: 25 Sep 2015, 16:29
-
 par Kolis » 08 Nov 2015, 19:09
par Kolis » 08 Nov 2015, 19:09
ilikoko123 a écrit:L'exercice demande une condition suffisante et necessaire sur a rt b pour que la matrice soit diagonalisable , faut montrer que si la matrice est diagonalisable alors ab est non nul et a est different de b , ie : le fait que le polynome caractéristique n'admet que des racines simples n'est pas une condition necessaire
Bonsoir !
La formule de récurrence donnée par Robot hier à 22h43 permet (par la méthode des suites récurrentes doubles) d'expliciter

.
L'équation caractéristique admet les racines distinctes

si
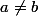
et la racine double

si

.
Donc, si
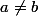
on a
=\alpha(X+a)^n+\beta(X+b)^n)
soit
=\dfrac{b(X+a)^n-a(X+b)^n}{b-a})
et, si

,
=(X+a)^n(\alpha+n\beta))
soit
=(X+a)^{n-1}\Bigl(X-(n-1)a\Bigr))
.
pas de problème pour diagonaliser si
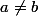
.
Supposons

. On note
_{1\le k\le n},\;s=\sum_{1\le k\le n}e_k)
de sorte que
=as-ae_k;\;u(s)=(n-1)as)
.

dirige l'espace propre associé à la valeur propre simple
a)
(c'est d'ailleurs évident).
Maintenant,
=-a(s-ne_k))
donc on a une base
_{2\le k\le n})
d'un espace de dimension

associé à la valeur propre

.
.....
il y a un bug : j'ai écrit "valeur propre -a " et je vois apparaître f(x)=x^2...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
. On soustrait la deuxième ligne de la première puis la deuxième colonne de la première. La première ligne a ses deux premiers coefficients
et
les autres sont nuls. On développe le déterminant suivant la première ligne. On a d'une part
fois le déterminant de
, d'autre part
fois le déterminant d'une matrice dont la première colonne a pour premier coefficient
et tous les autres coefficients nuls. Ce dernier déterminant est donc
fois le déterminant de
. En remettant tout ensemble,
pour
. Pour les deux premiers,
et
.
et
:
et
. (Indication : pour
,
.)
, si
est racine de
et
, alors
est aussi racine de
. En déduire que
et
n'ont pas de racine commune.
et en déduire que
est diagonalisable sur
.
