Critère diagonalisabilité

[ilikoko123]

est-ce possible :D ? directement en calculant le déterminant ?

[Robot]

Oui, c'est possible par récurrence.

[ilikoko123]

ben d'accord donnez moi un peu de temps :D

[Robot]

Un petit coup de pouce : il est commode d'avoir une relation de récurrence entre P(n), P(n-1) et P(n-2). Cette relation de récurrence suffit d'ailleurs à montrer ce qu'on veut, sans calculer explicitement P(n).

[ilikoko123]

pour ce la c'est sans doute qu'on va jouer sur les opération dans le determinant et developper suivant une rangée hein ?

[anouai]

Desolé
Mais j arrive pas a le resoudre
J ai calculé p(n=2) etp(n=3) et p(n=4) et j ai conclu p(n) en fonction de tous les p(i) tel que i€[1,n-1]
Et je sais qu on a trouvé que p'(n)=np(n-1)
Mais Quand je suppose que M est diagonalisable tel que M€Mn(R) je n arrive pas a conclure que pour M€Mn+1(R) M est diagonalisable :mur:

[Robot]

pour ce la c'est sans doute qu'on va jouer sur les opération dans le determinant et developper suivant une rangée hein ?

Oui, des petites manips sur les déterminants permettent d'établir une relation de récurrence sympa entre , et (pour supérieur ou égal à 2).
Cette relation de récurrence permet d'établir, sous l'hypothèse que est non nul et que est différent de , que n'a que des racines simples.

[ilikoko123]

d'accord , en faisant on developpe suivant la première ligne on trouve ce determinant en pointillés si on y effectue l'opération la première ligne ne contiendra qu'un terme non nul (-(X+a)) et en developpant suivant cette ligne je ne retrouve malheuseument pas 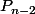, or ce determinant peut être facilement calculé. c'est facilement transformable en un determinant d'une matrice triangulaire , je ne sais pas ci cela peut mener à quelque chose , avez vous obtenu la relation de récurrence ?

[Robot]

Un bon début. Pourquoi ne pas faire aussi l'opération symétrique sur les colonnes ?

[ilikoko123]

Hélas je trouve

[ilikoko123]

[ilikoko123]

n'est ce pas correct ?

[Robot]

n'est ce pas correct ?

A vue de nez, non. J'ai dit , , .

[anouai]

P(2)=x**2-ab
P(3)=x(x**2_ab)-2abx-ab(a+b)
=>P(3)=xP(2)-2abP(1)-ab(a+b)
On generalise P(n)=xP(n-1)-2abP(n-2)-ab(a+b)
:-/ ?!

[Robot]

Non, tu n'y es pas du tout.
J'ai indiqué quelle manip faire sur le déterminant qui calcule . Ca n'a absolument rien de sorcier !

[ilikoko123]

Je suggère une seconde méthode, pourquoi ne pas ajouter une variable x a tous les termes du determinant et étudier la fonction de la variable x ?

[Robot]

Pour quoi faire ? Si tu as une autre méthode, vas-y je t'en prie.
Je suis un peu déçu que tu cales sur la relation de récurrence. C'est pourtant très simple. A mon avis, tu as fait une petite erreur bête dans ton calcul précédent (un décalage de 1 sur la dimension).

[ilikoko123]

??

[ilikoko123]

et ..
http://www.cjoint.com/c/EKho031k2J1

[MouLou]

Oui comme la méthode sur ce post:

http://www.maths-forum.com/propriete-determinant-168854.php

Apres je suis sur que la méthode que Robot te propose n'est pas si sorcier(ère)! :lol3: