Critère diagonalisabilité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Robot
 par Robot » 04 Nov 2015, 22:44
par Robot » 04 Nov 2015, 22:44
Tu jettes l'éponge pour n=3 ?
-
ilikoko123
- Membre Relatif
- Messages: 219
- Enregistré le: 09 Oct 2015, 21:40
-
 par ilikoko123 » 04 Nov 2015, 23:00
par ilikoko123 » 04 Nov 2015, 23:00
malheureusement :/
-
ilikoko123
- Membre Relatif
- Messages: 219
- Enregistré le: 09 Oct 2015, 21:40
-
 par ilikoko123 » 05 Nov 2015, 12:49
par ilikoko123 » 05 Nov 2015, 12:49
Bon.
Si a#b c'est clos
Si a=b on peut ecrire la matrice ainsi : M=a

-a
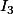
On a donc rg(M+aI)=1 d'ou dim ker(M+aI)=2 , ça prouve que la dimension du sous espace propre associé à -a est de dimension egale a la multiplicite de -a dans le polynome caractéristique et puis nous avons la diagonalisabilite ,ai je raison ?
-
Robot
 par Robot » 05 Nov 2015, 13:04
par Robot » 05 Nov 2015, 13:04
ilikoko123 a écrit:Bon.
Si a#b c'est clos
Tu as peut-être un argument pour ça, mais je n'en ai rien vu. Pourquoi c'est clos ?
ilikoko123 a écrit:Si a=b on peut ecrire la matrice ainsi : M=a

-a
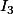
On a donc rg(M+aI)=1 d'ou dim ker(M+aI)=2 , ça prouve que la dimension du sous espace propre associé à -a est de dimension egale a la multiplicite de -a dans le polynome caractéristique et puis nous avons la diagonalisabilite ,ai je raison ?
Ca, OK. On peut généraliser ce résultat à la dimension n quelconque.
-
ilikoko123
- Membre Relatif
- Messages: 219
- Enregistré le: 09 Oct 2015, 21:40
-
 par ilikoko123 » 05 Nov 2015, 13:49
par ilikoko123 » 05 Nov 2015, 13:49
mais j'écrit sans réfléchir ! on ne peut pas étudier une fonction contenant deux termes complexes (a et b) sur R , là je suis vexé
-
ilikoko123
- Membre Relatif
- Messages: 219
- Enregistré le: 09 Oct 2015, 21:40
-
 par ilikoko123 » 05 Nov 2015, 13:53
par ilikoko123 » 05 Nov 2015, 13:53
même la méthode de cardan ne prend en compte que les équations a coefficients réels
-
Robot
 par Robot » 05 Nov 2015, 13:56
par Robot » 05 Nov 2015, 13:56
ilikoko123 a écrit:mais j'écrit sans réfléchir !
Ca, c'est un grand tort !
ilikoko123 a écrit:on ne peut pas étudier une fonction contenant deux termes complexes (a et b) sur R , là je suis vexé
Tu te vexes facilement !
Une suggestion : tu as calculé le polynôme caractéristique. Pourquoi n'essaies-tu pas de montrer que toutes ses racines (complexes) sont simples, sous les hypothèse
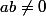
et
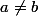
? Ca peut se faire en montrant que le polynôme caractéristique est premier avec son polynôme dérivé (par exemple, en calculant un pgcd).
-
Robot
 par Robot » 05 Nov 2015, 13:57
par Robot » 05 Nov 2015, 13:57
ilikoko123 a écrit:même la méthode de cardan ne prend en compte que les équations a coefficients réels
Ben non, voyons !
-
ilikoko123
- Membre Relatif
- Messages: 219
- Enregistré le: 09 Oct 2015, 21:40
-
 par ilikoko123 » 05 Nov 2015, 14:27
par ilikoko123 » 05 Nov 2015, 14:27
effectivement si on pose P le pgcd du polynome et de sa dérivée on trouve que P divise
X + (a+b)^2/2)
et
X +2ab)
en faisant la différence et puisque
^2)
et non nul on trouve le PGCD = 1
je voudrais juste vous demander d'ou des idées pareilles vous arrivent à l'esprit :fan: (ce pgcd par exemple)
-
Robot
 par Robot » 05 Nov 2015, 14:34
par Robot » 05 Nov 2015, 14:34
J'ai triché en calculant le discriminant. :lol3:
-
ilikoko123
- Membre Relatif
- Messages: 219
- Enregistré le: 09 Oct 2015, 21:40
-
 par ilikoko123 » 05 Nov 2015, 14:40
par ilikoko123 » 05 Nov 2015, 14:40
huh un discriminant de taille 3 !
malheureusement on n'a pas encore terminé
-
Robot
 par Robot » 05 Nov 2015, 16:03
par Robot » 05 Nov 2015, 16:03
Eh oui, il y a des discriminants pour des polynômes de n'importe quel degré.
Il serait peut-être intéressant maintenant de s'intéresser au polynôme caractéristique

pour la matrice de taille

.
On a
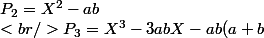\\<br />P_4={?})
Au fait, vois-tu une relation entre

et

?
-
Kolis
- Membre Relatif
- Messages: 482
- Enregistré le: 25 Sep 2015, 16:29
-
 par Kolis » 05 Nov 2015, 16:04
par Kolis » 05 Nov 2015, 16:04
Encore une lecture "rapide" : Robot parlait de "discriminant", ta remarque laisse entendre que tu as compris "déterminant"...
-
ilikoko123
- Membre Relatif
- Messages: 219
- Enregistré le: 09 Oct 2015, 21:40
-
 par ilikoko123 » 05 Nov 2015, 16:11
par ilikoko123 » 05 Nov 2015, 16:11
Kolis a écrit:Encore une lecture "rapide" : Robot parlait de "discriminant", ta remarque laisse entendre que tu as compris "déterminant"...
bah non je parlais du discriminant de l'equation de troisième degré

( ce "taille 3" était un simple raccourcis capable de créé des malentendus

)
-
ilikoko123
- Membre Relatif
- Messages: 219
- Enregistré le: 09 Oct 2015, 21:40
-
 par ilikoko123 » 05 Nov 2015, 16:44
par ilikoko123 » 05 Nov 2015, 16:44
oué en fait si on démontre que

alors le chemin de récurrence apparait en supposant que
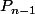
est scindé à racines simple , et en montrons que
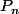
l'est aussi
-
Robot
 par Robot » 05 Nov 2015, 16:48
par Robot » 05 Nov 2015, 16:48
Prends le temps de bien réfléchir.
-
ilikoko123
- Membre Relatif
- Messages: 219
- Enregistré le: 09 Oct 2015, 21:40
-
 par ilikoko123 » 05 Nov 2015, 16:54
par ilikoko123 » 05 Nov 2015, 16:54
ok :D ......
-
ilikoko123
- Membre Relatif
- Messages: 219
- Enregistré le: 09 Oct 2015, 21:40
-
 par ilikoko123 » 05 Nov 2015, 17:45
par ilikoko123 » 05 Nov 2015, 17:45
c'est embarrassant j'arrive pas a grand chose , en effet j'ai essayé d'exploiter

j 'ai supposé que Pn-1 est à racines simples ( sans parler de scindé car on est dans C) et puis je n'ai pu montrer que le fait que tous les racines de Pn ont une multiplicité au plus deux
une autre approche m'a apparu c'est de montrer que
=1)
par recurence sur n , mais j'ai pas pu faire apparaitre
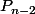
comme combinaison de Pn et Pn-1 pour conclure :hum: je suis sur qu'une étape intéressante méchappe
-
ilikoko123
- Membre Relatif
- Messages: 219
- Enregistré le: 09 Oct 2015, 21:40
-
 par ilikoko123 » 05 Nov 2015, 19:28
par ilikoko123 » 05 Nov 2015, 19:28
:help: ....
-
Robot
 par Robot » 05 Nov 2015, 21:21
par Robot » 05 Nov 2015, 21:21
Peux-tu calculer

?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités
 -a
-a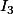
-a
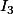
 j 'ai supposé que Pn-1 est à racines simples ( sans parler de scindé car on est dans C) et puis je n'ai pu montrer que le fait que tous les racines de Pn ont une multiplicité au plus deux
j 'ai supposé que Pn-1 est à racines simples ( sans parler de scindé car on est dans C) et puis je n'ai pu montrer que le fait que tous les racines de Pn ont une multiplicité au plus deux =1) par recurence sur n , mais j'ai pas pu faire apparaitre
par recurence sur n , mais j'ai pas pu faire apparaitre 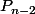 comme combinaison de Pn et Pn-1 pour conclure :hum: je suis sur qu'une étape intéressante méchappe
comme combinaison de Pn et Pn-1 pour conclure :hum: je suis sur qu'une étape intéressante méchappe