Critère de Cauchy

[legeniedesalpages]

Bonsoir,

je bloque sur cet exercice:

On considère une suite de nombre réels telle que
[CENTER], pour tout .[/CENTER]
Montrer à l'aide du critère de Cauchy, que est convergente lorsque .

Je ne vois pas comment montrer que est de Cauchy.

Merci pour vos indications.

[Joker62]

ça semble correct non ?

[fahr451]

bonsoir

je présume que c'est un n-1 à droite et non n+1


| x(n+1) - x(n)| =< k^n |x(1) -x(0) |

la série de droite converge (géométrique) donc la série

sigma (x(n+1) -x(n) ) converge absolument donc converge et la suite x(n) converge

si tu veux vraiment écrire le critère de cauchy

|x(n+p) - x(n) | = <(k^(n+p-1) + k^(n+p-2) +...+k^n)|x(1) -x(0) |

=< k^n (1+k +...jusqu'à l'infini) |x(1) -x(0) | = |x(1)-x(0)|k^n/(1-k)
qu'on peut rendre inférieur à epsilon pour n assez grand

[legeniedesalpages]

ah ok, je vois. Merci pour votre aide :)

[fahr451]

ça semble correct non ?

ben non a priori c'est une somme de puissances de k

[Joker62]

Pardon ?
Y'a quoi qui va pas :( ?

Mise à part que ça se termine pas par x_1 - x_0 ( suffit de continuer dans ce cas na ) ?

[legeniedesalpages]

Bonjour Joker,

dans la première égalité au membre de gauche il faut rajouter dans la valeur absolue:

(sinon il n'y a pas forcément égalité)

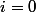
ensuite membre droit de la premiere inégalité, la somme est de à et non , la dernière inégalité, je ne vois pas d'où elle sort.

[Joker62]

Vui j'ai compris :D
Comme dit fahr c'est la somme des puissances de k :o

Désolé :)