Milles excuses je n'avais pas remarqué !
L'expression est :
^{j+1} \epsilon_{t+j+1};\epsilon_{t+1}]))
Et oui epsilon est bien un bruit blanc !
Ah zut je viens de me rendre compte que je n'ai pas fini les calculs, je ne sais pas ce qui m'arrive... :mur:
Voici les expressions complètes :
 = cov(\epsilon_t + \theta_1 \epsilon_{t-1} +\theta_2 \epsilon_{t-2} ; \epsilon_{t+1} +\theta_1 \epsilon_t + \theta_2 \epsilon_{t-1}))
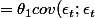 +\theta_2 cov(\epsilon_{t-1};\epsilon_{t-1}))
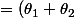\sigma^2_{\epsilon})
 = cov(\epsilon_t + \theta_1 \epsilon_{t-1} +\theta_2 \epsilon_{t-2} ; \epsilon_{t+2} +\theta_1 \epsilon_{t+1} + \theta_2 \epsilon_{t}))
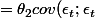)
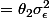
L'énoncé est :
Soit le processus
 : X_t = \epsilon_t + \theta_1 \epsilon_{t-1} + \theta_2 \epsilon_{t-2})
1) est-il stationnaire ?
Réponse : oui car tout processus MA(q) est stationnaire.
2) Caractériser son auto corrélogramme
Et la c'est les développement au dessus, pour etre franc je ne comprends pas trop ce qu'on nous demande, mais comprendre les calculs pourrait m'être d'une grande aide !
Voila merci et encore désolé pour la faute !
PS : je précise que l'expression en haut et ce qui suit n'est pas lié !
