Bonjour,
Sur l'article "courbure" de wikipedia au paragraphe "Définition de la courbure d'un arc plan" il est écrit d²r/ds²= tout un truc avec r(t) et ses derivées par rapport à t, sachant que s est l'abcisse curviligne et r le vecteur position d'un mobile exprimé en fonction de t ou s.
bref voici le lien: http://fr.wikipedia.org/wiki/Courbure
Comment montrer cette relation?
(l'interet que j'y vois est de comprendre pourquoi la courbure correspond à la norme du vecteur acceleration si on parcours la courbe à la vitesse constante =1=ds/dt)
merci
Courbure d'un arc plan
2 messages
- Page 1 sur 1
Bonjour,
Si je comprends bien, la question est : pourquoi un changement de paramètre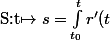dt$) permet d'avoir un vecteur vitesse de norme égale à 1. En effet, si la norme du vecteur vitesse est constante, les variations du vecteur vitesse se font orthogonalement à celui-ci, cela correspondra bien à l'idée qu'on se fait de la courbure.
permet d'avoir un vecteur vitesse de norme égale à 1. En effet, si la norme du vecteur vitesse est constante, les variations du vecteur vitesse se font orthogonalement à celui-ci, cela correspondra bien à l'idée qu'on se fait de la courbure.
On étudie un arc équivalent à
un arc équivalent à  .
.
=\frac{d}{dt}(\bar{r}oS)=\frac{dS}{dt}.<br />\frac{d\bar{r}}{ds}=||r'(t)||\frac{d\bar{r}}{ds}$)
||}r'(t)$)

Si je comprends bien, la question est : pourquoi un changement de paramètre
On étudie
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
