Courbes polaires
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Emmanuelle89
- Membre Naturel
- Messages: 13
- Enregistré le: 22 Nov 2007, 19:59
-
 par Emmanuelle89 » 22 Nov 2007, 20:03
par Emmanuelle89 » 22 Nov 2007, 20:03
on considère la courbe polaire :
r=cos^3(t)-sin^3(t)
(t=théta)
on me demande de déduire de r(t)/r'(t) les points de C pour lesquels la tangente à C est de pente 1.
ça serait vraiment sympa de m'aider, je n'en peux plus...
 par busard_des_roseaux » 22 Nov 2007, 21:01
par busard_des_roseaux » 22 Nov 2007, 21:01
salut,
Un peu de cours:Soit M de coordonnées polaire(r,t).
On prend comme repère du plan
,sin(t)))
et
;cos(t))=\frac{du}{dt})
M a pour équation
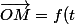 \vec{u(t)})
On dérive pour obtenir le vecteur vitesse:
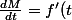 \vec{u} +f(t) \vec{v})
Au points de pente 1,

est colinéaire à
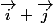
 (-sin(t))-3 sin^{2}(t) cos(t) \right) \left( \cos(t) \vec{i}+\sin(t)\vec{j} \right) + \left( \cos^3(t) - sin^{3}(t) \right) \left( -\sin(t) \vec{i}+\cos(t)\vec{j} \right))
doit être proportionnel à
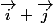
-
Emmanuelle89
- Membre Naturel
- Messages: 13
- Enregistré le: 22 Nov 2007, 19:59
-
 par Emmanuelle89 » 22 Nov 2007, 21:06
par Emmanuelle89 » 22 Nov 2007, 21:06
ok mais comment se servir de r'/r?
 par busard_des_roseaux » 22 Nov 2007, 21:29
par busard_des_roseaux » 22 Nov 2007, 21:29
busard_des_roseaux a écrit:On dérive pour obtenir le vecteur vitesse:
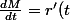 \vec{u} +r(t) \vec{v})

a pour coord:
 \cos(t) -r(t) \sin(t) \\<br />r'(t) \sin(t) + r(t) \cos(t) <br />\end{array}<br />\right)
d'où les points cherchés verifient:
 \cos(t) -r(t) \sin(t) = r'(t) \sin(t) + r(t) \cos(t))
-
Emmanuelle89
- Membre Naturel
- Messages: 13
- Enregistré le: 22 Nov 2007, 19:59
-
 par Emmanuelle89 » 22 Nov 2007, 21:30
par Emmanuelle89 » 22 Nov 2007, 21:30
ok je suis toujours...
 par busard_des_roseaux » 22 Nov 2007, 21:36
par busard_des_roseaux » 22 Nov 2007, 21:36
 \left( \cos(t) - \sin(t) \right) = r(t) ( \sin(t) + \cos(t) ))
il faut dériver et remplacer.
il vient:
cos(t) \left( cos(t)+sin(t)) (cos(t)-sin(t))=<br />(cos^3(t)-sin^3(t))(sin(t)+cos(t)))
1ère famille de solutions:
cos(t)+sin(t)=0
2ème famille de solutions:
cos(t)-sin(t)=0
sinon, on simplifie:
cos(t) =<br />(cos^2(t) + cos(t)sin(t) + sin^2(t))
soit:
 + sin^(t) \right)}^2=0)
-
Emmanuelle89
- Membre Naturel
- Messages: 13
- Enregistré le: 22 Nov 2007, 19:59
-
 par Emmanuelle89 » 22 Nov 2007, 21:45
par Emmanuelle89 » 22 Nov 2007, 21:45
oui puis je me suis servie de l'expression que j'ai trouvé pour r'/r, j'ai aboutie à
[-3costsint]/(1-sintcost)=0
j'ai déduis que t=kpi k étant relatif ou t=pi/2 [2Pi]...
oups je trouve pas comme vous :s
je vais recalculer
 par busard_des_roseaux » 22 Nov 2007, 21:53
par busard_des_roseaux » 22 Nov 2007, 21:53
1ère famille de solutions:
cos(t)+sin(t)=0
je multiplie par
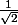
, ça devient:
=0)
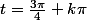
2ème famille de solutions:
-sin(t)=0)
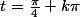
ce sont les deux mêmes familles, doù:
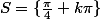
sauf erreur :hum:
:dodo: :triste: :dodo:
-
Emmanuelle89
- Membre Naturel
- Messages: 13
- Enregistré le: 22 Nov 2007, 19:59
-
 par Emmanuelle89 » 22 Nov 2007, 21:57
par Emmanuelle89 » 22 Nov 2007, 21:57
quand on m'a dit de calculer r/r' à la question précédente j'ai
r/r'=[(cost-sint)(1+sintcost)]/[(-3sintcost)(sint+cost)]
et en remplaçant dans
r'sint+rcost=r'cost-rsint
je trouve
-3costsint/(1+sintcost)=0
...
 par busard_des_roseaux » 22 Nov 2007, 22:01
par busard_des_roseaux » 22 Nov 2007, 22:01
Emmanuelle89 a écrit:quand on m'a dit de calculer r/r' à la question précédente j'ai
r/r'=[(cost-sint)(1+sintcost)]/[(-3sintcost)(sint+cost)]
je suis d'accord. tu peux vérifier les calculs en
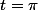
par exemple
pour voir s'ils sont justes.salut. :dodo:
-
Emmanuelle89
- Membre Naturel
- Messages: 13
- Enregistré le: 22 Nov 2007, 19:59
-
 par Emmanuelle89 » 22 Nov 2007, 22:34
par Emmanuelle89 » 22 Nov 2007, 22:34
merci beaucoup! vous m'avez repêchée d'un désespoir digne d'un soir de pluie où il faut arriver à faire un dm pour le lendemain matin sans dépasser 23h...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
