Courbe point stationnaire
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
par novicemaths » 26 Mar 2021, 21:12
Bonsoir
Voici un exercice sur les points stationnaires.
=2t^{11}-t^9+2t^8-2t^7+3t^6+2t^5-t^4-2t^3-2)
=t^{11}-3t^{10}+3t^9-2t^8-3t^6+2t^5+2t^4-2t^3-1)
Pour
)
, on écrit
M = (x,y)=0 sur
CCalculer le plus petit indice de p>0 et pour lequel
est non nul. Que vaut
J'ai commencé par dériver.
=22t^{10}-9t^8+16t^7-14t^6+18t^5+10t^4-4t^3-6t^2)
=11t^{10}-30t^9+27t^8-16t^7-18t^5+10t^4+8t^3-6t^2)
Dois-je faire une dérivation successive pour trouver p>0 et
?
Dans mes cours, les points stationnaires sont plus simple, j'ai trouvé cette exercice sur un annale d'examen du Maroc.
A bientôt
-
phyelec
- Habitué(e)
- Messages: 985
- Enregistré le: 06 Mar 2020, 16:47
-
par phyelec » 26 Mar 2021, 22:49
Bonjour,
vous faites l'étude au point (-1,-1)?
vous devez faire un développement de Taylor de x(t) et y(t) pour t0=-1 pour trouver p et q.
-
phyelec
- Habitué(e)
- Messages: 985
- Enregistré le: 06 Mar 2020, 16:47
-
par phyelec » 26 Mar 2021, 22:56
p impair et q pair : point ordinaire.
p impair et q impair : point d’inflexion
p pair et q impair : point de rebroussement de 1ère espèce
p pair et q pair : point de rebroussement de 2nd espèce
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
par novicemaths » 27 Mar 2021, 14:51
Bonjour
Le développement limité doit être de quel ordre exactement ?
A bientôt
-
phyelec
- Habitué(e)
- Messages: 985
- Enregistré le: 06 Mar 2020, 16:47
-
par phyelec » 27 Mar 2021, 16:44
(p; q) les plus petits possibles.
p est le rang de dérivation du premier vecteur dérivé non nul. ( le vecteur formé par
})
et
})
que l'on peut appeler
})
q est le rang du premier vecteur dérivé non colinéaire que l'on peut appeler
})
on q>p
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
par novicemaths » 27 Mar 2021, 20:06
Donc, il faut que je dérive deux fois ?
A bientôt
-
phyelec
- Habitué(e)
- Messages: 985
- Enregistré le: 06 Mar 2020, 16:47
-
par phyelec » 27 Mar 2021, 23:04
je trouve p=1, car x'(-1)=-27 et y'(-1)=98 donc différents de 0.
je trouve q=2, car x''(-1)=-168et y''(-1)=-808 non colinéaire au vecteur de coordonnée x'(-1) et y'(-1).
Vérifiez mes calculs quand même.
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
par novicemaths » 28 Mar 2021, 21:00
Bonsoir
Voici les calculs que j'ai réalisé, il y a surement des erreurs.
=22(-1)^{10}-9(-1)^{8}+16(-1)^7-14(-1)^6+10(-1)^4-6(-1)^3=-1)
=11(1)^{10}-30(1)^9+27(1)^8-16(1)^7-18(1)^5+10(1)^4+8(1)^3-6(1)^2=-14)
=220(-1)^9-72(-1)^8-84(-1)^5+40(-1)^3-12(-1)^2-12(-1)=-248)
=110(1)^9-270(1)^8-172(1)^6-90(1)^4+40(1)^3+24(1)^2-12(1)=-370)
Alors p=1 et
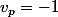
A bientôt
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
