Courbe elliptique

[mehdi-128]

Bonjour, je ne comprends pas la définition suivante :

En mathématiques, une courbe elliptique est un cas particulier de courbe algébrique, munie entre autres propriétés d'une addition géométrique sur ses points.

Pareil pour la courbe elliptique :

En mathématiques, et plus précisément en géométrie algébrique, une courbe algébrique est une variété algébrique (ou un schéma de type fini) sur un corps, dont les composantes irréductibles sont de dimension 1.

Je ne vois pas du tout.

Cordialement.

[Doraki]

Ca dépend de pourquoi tu veux savoir ce qu'est une courbe elliptique et de comment t'es tombé sur ces définitions, mais si tu veux les comprendre, ptetre que tu devrais lire une introduction à la géométrie algébrique ?

[mehdi-128]

En regardant une émission sur la personne qui avait démontré le théorème de Fermat.

Je veux juste savoir ce que ça signifie en gros sans rentrer dans les équations.

J'ai jamais vu ça en MPSI-MP...

Je sais pas ça fait partie de quel programme.

[mehdi-128]

On appelle plan projectif sur un corps K l'ensemble P^2(K) des classes d'équivalence (K^3 -(0,0,0,)/R ou R est une relation d'équivalence définie par :

Pour tout (a,b,c) (a',b',c') de K :

(a,b,c)R(a',b',c') Il existe t app K\{0}, (a,b,c)=t(a',b',c')

Ca signifie quoi le (K^3 -(0,0,0,)/R ?

Je comprends rien à l'histoire d'équivalence.

Et aussi ils disent que ça revient à projeter l'espace sur une demi sphère centrée en (0,0,0) pourquoi ?

[deltab]

Bonsoir.

On appelle plan projectif sur un corps K l'ensemble P^2(K) des classes d'équivalence (K^3 -(0,0,0,)/R ou R est une relation d'équivalence définie par :

Pour tout (a,b,c) (a',b',c') de K :

(a,b,c)R(a',b',c') Il existe t app K\{0}, (a,b,c)=t(a',b',c')

Ca signifie quoi le (K^3 -(0,0,0,)/R ?

Je comprends rien à l'histoire d'équivalence.

Et aussi ils disent que ça revient à projeter l'espace sur une demi sphère centrée en (0,0,0) pourquoi ?

(K^3 -(0,0,0,)/R est l'espace quotient: R désigne la relation d'équivalence noté R auparavant (sans le gras). Au fait pourquoi tu as écrit R en gras? Pour qu'il n'y ait d'ambiguïté dans l'écriture, il faudra ajouter la parenthèse manquante en revenant à la notation habituelle d'une relation 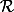et non R.