Bonjour, je viens solliciter votre aide pour un petit exo de proba que j'ai cherché :)
Le voici :
On donne un entier n supérieur ou égal à 3. n personnes se répartissent au hasard dans 3 pièces A_1, A_2 et A_3, chaque pièce pouvant contenir de 0 à n personnes.
On désigne par X_1, X_2 et X_3 les v.a. prenant pour valeurs respectives le nombre de personnes situées dans les pièces A_1, A_2 et A_3.
1/ a/ Donner les lois de probabilités de X_1, X_2, X_3 et X_1+X_2.
J'ai trouvé : P(X_1 = k) = P(X_2 = k) = P(X_3 = k) = (k parmi n)/2^n
Et : P(X_1+X_2 = k) = P(X_3 = n-k) = (n-k parmi n)/2^n = (k parmi n)/2^n
b/ Déterminer la variance de X_1+X_2 ; en déduire la covariance du couple (X_1, X_2).
J'ai trouvé : V(X_1+X_2) = V(n - X_3) = V(X_3)
Pour E(X_3(X_3 - 1)) je trouve : n(n-1)/4
et pour E(X_3) : n/2
D'où V(X_3) = n(n-1)/4 + n/2 - n²/4 = n/4
Et Cov(X_1, X_2) = V(X_1 + X_2) - V(X_1) - V(X_2) = n/4 - n/2 - n/2 = - n/4
Dites moi s'il y a des erreurs jusques là svp...
Ensuite on me dit :
2/ Donner la loi de probabilité conjointe du couple (X_2, X_3), mais je sais pas trop comment faire...
J'ai fait ceci :
P[(X_2, X_3) = (p, q)] = P([X_2 = p]INTER[X_3 = q]) (pour p + q =< n)
= P(X_2 = p sachant que X_3 = q) P(X_3 = q)
= (p parmi n-q)/2^(n-q) * (q parmi n)/2^n
= n!/(p! q! (n-q-p)! 2^(2n-q))
C'est ça ??
Et enfin :
Soit Y_n la v.a. prenant pour valeurs le nombre de pièces occupés (1, 2 ou 3).
Donner la loi de Y_n :
P(Y_n = 1) = 3/2n
P(Y_n = 2) = P(X_1 = 0) + P(X_2 = 0) + P(X_3 = 0) - P(Y_n = 1) = ... 0 ??
Et là je me dis que j'ai dû me planter dès le début, mais j'arrive pas à me corriger...
Merci de votre aide.
PS : désolé d'avoir posté dans "Lycée", je me suis trompé...
Couples de VAR
26 messages
- Page 1 sur 2 - 1, 2
par les TPEistes » 17 Avr 2009, 18:18
Je connais rien en Latex, mais si tu connais un tuto sympa je veux bien aller voir ça :happy2:
par les TPEistes » 17 Avr 2009, 20:48
Hop ! Et voila !!
On donne un entier n supérieur ou égal à 3. n personnes se répartissent au hasard dans 3 pièces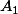
, 
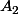et 
, chaque pièce pouvant contenir de 0 à n personnes.
On désigne par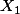
, 
et 
les v.a. prenant pour valeurs respectives le nombre de personnes situées dans les pièces 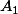, 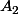et .
1/ a/ Donner les lois de probabilités de
et 
.
J'ai trouvé : = P(X_{2} = k) = P(X_{3} = k) = \frac{\begin{pmatrix}<br />n \\<br />k<br />\end{matrix}}{2^n})
Et : = P(X_{3}= n-k) = \frac{\begin{pmatrix}<br />n \\<br />n-k<br />\end{matrix}}{2^n} = \frac{\begin{pmatrix}<br />n \\<br />k<br />\end{matrix}}{2^n})
b/ Déterminer la variance de ; en déduire la covariance du couple (
).
J'ai trouvé : = V(n - X_{3}) = V(X_{3}))
Pour))
je trouve : }{4})
et pour)
: 
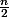
D'où = \frac{n(n-1)}{4} + \frac{n}{2} - \frac{n^2}{4} = \frac{n}{4})
Et = V(X_{1} + X_{2}) - V(X_{1}) - V(X_{2}) = \frac{n}{4} - \frac{n}{4} - \frac{n}{4} = - \frac{n}{4})
Dites moi s'il y a des erreurs jusques là svp...
Ensuite on me dit :
2/ Donner la loi de probabilité conjointe du couple (
), mais je sais pas trop comment faire...
J'ai fait ceci :
 = (p, q)] = P([X_{2} = p]\cap[X_{3} = q]))
)
}(X_{2} = p) P(X_{3} = q))
! 2^{2n-q}})
C'est ça ??
Et enfin :
Soit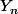
la v.a. prenant pour valeurs le nombre de pièces occupés (1, 2 ou 3).
Donner la loi de: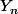
 = \frac{3}{2n})
 = P(X_{1} = 0) + P(X_{2} = 0) + P(X_{3} = 0) - P(Y_{n} = 1) = ... 0 ??)
Et là je me dis que j'ai dû me planter dès le début, mais j'arrive pas à me corriger...
On donne un entier n supérieur ou égal à 3. n personnes se répartissent au hasard dans 3 pièces
On désigne par
1/ a/ Donner les lois de probabilités de
J'ai trouvé :
Et :
b/ Déterminer la variance de
J'ai trouvé :
Pour
et pour
D'où
Et
Dites moi s'il y a des erreurs jusques là svp...
Ensuite on me dit :
2/ Donner la loi de probabilité conjointe du couple (
J'ai fait ceci :
C'est ça ??
Et enfin :
Soit
Donner la loi de
Et là je me dis que j'ai dû me planter dès le début, mais j'arrive pas à me corriger...
par nuage » 17 Avr 2009, 22:20
Salut,
en effet ton calcul de)
est faux.
Pour s'en convaincre il suffit de regarder le cas
:
on a de façon évidente=\frac23)
Pour faire le calcul :
Le nombre d'éléments de l'univers est le nombre d'applications d'un ensemble à
éléments (les personnes) dans un ensemble à 3 éléments (les pièces). Donc il y a 
cas possibles.
Pour placer
personnes dans une pièce il faut les choisir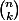 
possibilités, puis placer les 
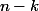restantes dans les deux autres pièces 
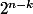possibilités.
je te laisse continuer, avec quand même une remarque sur le calcul de l'espérance. Par symétrie les trois espérances sont égales. Et leur somme est l'espérance de la somme soit ...
en effet ton calcul de
Pour s'en convaincre il suffit de regarder le cas
on a de façon évidente
Pour faire le calcul :
Le nombre d'éléments de l'univers est le nombre d'applications d'un ensemble à
Pour placer
je te laisse continuer, avec quand même une remarque sur le calcul de l'espérance. Par symétrie les trois espérances sont égales. Et leur somme est l'espérance de la somme soit
par les TPEistes » 18 Avr 2009, 09:18
Bonjour et merci de la réponse.
Donc on a :
 = P(X_{2} = k) = P(X_{3} = k) = \frac{\begin{pmatrix}<br />n \\<br />k<br />\end{matrix}}{3^n})
Et : = P(X_{3}= n-k) = \frac{\begin{pmatrix}<br />n \\<br />n-k<br />\end{matrix}}{3^{n-k}} = \frac{\begin{pmatrix}<br />n \\<br />k<br />\end{matrix}}{3^{n-k}})
c'est bien ça ?
Ensuite si j'ai bien compris ce que tu as dit :
 = E(n) = n)
Et donc :
 = E(X_{2}) = E(X_{3}) = \frac{n}{3})
En fait il s'agit de déterminer)
Je peux dire que c'est)
?
Si oui ça me donner = V(X_{3}))
et je n'ai plus qu'à calculer )
?
Donc on a :
Et :
Ensuite si j'ai bien compris ce que tu as dit :
Et donc :
En fait il s'agit de déterminer
Je peux dire que c'est
Si oui ça me donner
par nuage » 18 Avr 2009, 10:05
Salut,
non.
 = P(X_{2} = k) = P(X_{3} = k) = \frac{\begin{pmatrix}<br />n \\ k \end{matrix}2^{n-k}}{3^n})
Il ne faut pas oublier de répartir les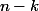 restants dans les deux autres pièces.
On peut remarquer que
^n = 3^n)
avec ton résultat la somme des probabilités n'est pas 1.
C'est ça
les TPEistes a écrit:Bonjour et merci de la réponse.
Donc on a :
non.
Il ne faut pas oublier de répartir les
On peut remarquer que
avec ton résultat la somme des probabilités n'est pas 1.
les TPEistes a écrit:Ensuite si j'ai bien compris ce que tu as dit :
Et donc :
En fait il s'agit de déterminer
Je peux dire que c'est
Si oui ça me donner
C'est ça
par les TPEistes » 18 Avr 2009, 10:31
Ok et donc :
 = P(X_{3}= n-k) = \frac{\begin{pmatrix}<br />n \\<br />n-k<br />\end{matrix}2^k}{3^n} = \frac{\begin{pmatrix}<br />n \\<br />k<br />\end{matrix}2^k}{3^n})
??
Après je trouve :
) = \frac{4n(n-1)}{9})
Et donc :
 = E(X_{3}(X_{3}-1) + E(X_{3}) - [E(X_{3})]^2 = \frac{4n(n-1)}{9} + \frac{3n}{9} - \frac{n^2}{9} = \frac{3n^2 - n}{9} = V(X_{1} + X_{2}))
Puis :
 = V(X_{1} + X_{2}) - V(X_{1}) - V(X_{2}) = \frac{n(3n-1)}{9} - \frac{n}{3} - \frac{n}{3} = \frac{3n^2 - 7n}{9})
Tu peux confirmer jusque là ?
Merci en tout cas !
??
Après je trouve :
Et donc :
Puis :
Tu peux confirmer jusque là ?
Merci en tout cas !
par nuage » 18 Avr 2009, 11:36
les TPEistes a écrit:Ok et donc :
je trouve la même chose.
Après je trouve :
je ne suis pas d'accord.
Je ne sais pas exactement comment tu fais ton calcul, mais je suppose que tu utilises la fonction génératrice de
Ensuite
Et donc :
Puis :
Tu peux confirmer jusque là ?
Merci en tout cas !
Comme le résultat précédent est faux c'est faux.
On peut faire un raisonnement un peu plus rapide en remarquant que
d'où
par les TPEistes » 18 Avr 2009, 12:45
Je ne connais pas la fonction génératrice. J'ai fait :
) = \sum_{k=0}^n k(k-1) P(X_3=k) = \sum_{k=2}^n k(k-1) P(X_3=k) = \frac{1}{3^n} \sum_{k=2}^n \frac{n!}{(k-2)!(n-k)!} 2^{n-k} = \frac{n(n-1)}{3^n} \sum_{k=2}^n \frac{(n-2)!}{(k-2)!(n-k)!} 2^{n-k} = \frac{4n(n-1)}{3^n} \sum_{k=0}^{n-2} {n-2 \choose k} 2^{n-k-2} 1^k = \frac{4n(n-1)}{3^n} 3^{n-2} = \frac{4n(n-1)}{9})
EDIT : ah oui je me suis trompé dans la Cov, donc la Cov je trouve}{9})
(avec mon calcul) ou 
(avec ton résultat).
EDIT : ah oui je me suis trompé dans la Cov, donc la Cov je trouve
par nuage » 18 Avr 2009, 13:43
J'ai dis une bêtise :briques:
Toujours est-il qu'il est facile de regarder des cas avec n petit (n=3 ou n=4)
Je vais essayer de relire ton calcul pour trouver l'erreur.
Toujours est-il qu'il est facile de regarder des cas avec n petit (n=3 ou n=4)
Je vais essayer de relire ton calcul pour trouver l'erreur.
par les TPEistes » 18 Avr 2009, 13:46
D'accord. Donc mon calcul est juste ? Comment se fait-il que je ne trouve pas la même chose que toi avec la fonction génératrice ? :o
par nuage » 18 Avr 2009, 14:19
les TPEistes a écrit:Je ne connais pas la fonction génératrice. J'ai fait :
L'erreur est dans cette égalité :
On a, en prenant
par les TPEistes » 18 Avr 2009, 14:39
Ah oui ! Là je suis d'accord.
Donc on obtient :
 = V(X_3) = \frac{2n}{9})
et :
 = \frac{-2n}{9})
Pour la suite :
2/ Donner la loi de probabilité conjointe du couple ()
J'ai fait ceci :
! 3^{n}})
Je suis pas certain pour}(X_{2} = p))
Qu'en dis-tu ?
Donc on obtient :
et :
Pour la suite :
2/ Donner la loi de probabilité conjointe du couple (
J'ai fait ceci :
Je suis pas certain pour
Qu'en dis-tu ?
par les TPEistes » 18 Avr 2009, 15:10
Bien donc ensuite :
Soit la v.a. prenant pour valeurs le nombre de pièces occupés (1, 2 ou 3).
Donner la loi de:
 = P(X_{1} = n) + P(X_{2} = n) + P(X_{3} = n) = \frac{1}{3^{n-1}})
 = P(X_{1} = 0) + P(X_{2} = 0) + P(X_{3} = 0) - P(Y_{n} = 1) = 3 (\frac{2}{3})^n - \frac{1}{3^{n-1}} = \frac{2^n-1}{3^{n-1}})
Et enfin :
 = 1 - P(Y_{n} = 1) - P(Y_{n} = 2) = \frac{3^{n-1}-2^n}{3^{n-1}})
C'est toujours bon ?
Soit
Donner la loi de
Et enfin :
C'est toujours bon ?
par nuage » 18 Avr 2009, 15:16
je ne crois pas :
pour on aurait la certitude d'avoir 2 pièces occupées ce qui est gênant.
pour
26 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :