[Trigonometrie] a+b+c=π et Cosinus
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Shadoww
- Membre Naturel
- Messages: 14
- Enregistré le: 12 Sep 2012, 14:59
-
 par Shadoww » 12 Sep 2012, 15:19
par Shadoww » 12 Sep 2012, 15:19
Merci de passer par là =)
Je cherche un "debloquage" devant mon equation qu'on me demande de resoudre :
Sachant a, b, c trois réels, et que
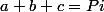
, montrer que :
^2+cos(b)^2+cos(c)^2+2cos(a)cos(b)cos(c) = 1)
Au fur et à mesure où j'avance, ma formule s'agrandit (En commençant par développer les carrés, pas sûr que ça soit la bonne méthode, mais ils me coincent à chaque fois.. ) et je me retrouve avec :
cos(b)-sin(a)sin(b))+(cos(2c)+4cos(a)cos(b)cos(c)+3)/2 = 1)
Bref, un peu n'importe quoi :triste:
J'utilise à peine les formules de bases de la trigonométrie (
http://gilles.costantini.pagesperso-orange.fr/Lycee_fichiers/CoursT_fichiers/formtrig.pdf par exemple ), et rien dans mon cours ne semble être la "baguette magique" de cette équation =/
Merci d'avance à tous !
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 12 Sep 2012, 15:29
par Arnaud-29-31 » 12 Sep 2012, 15:29
Bonjour,
As tu commencé par remplacer

par
)
?
-
Shadoww
- Membre Naturel
- Messages: 14
- Enregistré le: 12 Sep 2012, 14:59
-
 par Shadoww » 12 Sep 2012, 15:58
par Shadoww » 12 Sep 2012, 15:58
Arnaud-29-31 a écrit:Bonjour,
As tu commencé par remplacer

par
)
?
Mmh, et je remplace C partout ?
Ca m'enleve deja une variable, je vais voir ca =) Merci ^^
^2+cos(b)^2+cos(c)^2+2cos(a)cos(b)cos(c) = 1 (E))
Or, comme
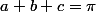
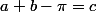
 cos(a)^2+cos(b)^2+cos(a+b-\pi)^2+2cos(a)cos(b)cos(a+b-\pi))
^2+cos(b)^2+(1+cos(2a+2b-2\pi)+2cos(a)cos(b)(cos(a+b)cos(\pi)+sin(a+b)sin(\pi)))
^2+cos(b)^2+(1+(cos(2a+2b)cos(2\pi)+sin(2a+2b)sin(2\pi))+2cos(a)cos(b)((cos(a)cos(b)-sin(a)sin(b))cos(\pi)+(sin(a)cos(b)+sin(b)cos(a)))sin(\pi)))
Ca va pour l'instant ? =X Parce que ca s'agrandit =S
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 12 Sep 2012, 17:51
par Arnaud-29-31 » 12 Sep 2012, 17:51
Shadoww a écrit:Or, comme
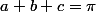
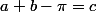
Attention, c'est dommage de partir sur une erreur comme ça !
-
Shadoww
- Membre Naturel
- Messages: 14
- Enregistré le: 12 Sep 2012, 14:59
-
 par Shadoww » 12 Sep 2012, 18:27
par Shadoww » 12 Sep 2012, 18:27
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 12 Sep 2012, 18:53
par Arnaud-29-31 » 12 Sep 2012, 18:53
Oula, il ne faut pas développer sans avoir une idée de où tu vas, la ca devient clairement pire que ce qu'on a au début.
De plus, est ce que tu maitrises les propriété de base de la fonction sur laquelle on travaille ?
))
ca ne se simplifie pas ?
-
Shadoww
- Membre Naturel
- Messages: 14
- Enregistré le: 12 Sep 2012, 14:59
-
 par Shadoww » 12 Sep 2012, 19:02
par Shadoww » 12 Sep 2012, 19:02
-
Shadoww
- Membre Naturel
- Messages: 14
- Enregistré le: 12 Sep 2012, 14:59
-
 par Shadoww » 12 Sep 2012, 20:04
par Shadoww » 12 Sep 2012, 20:04
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 12 Sep 2012, 20:18
par Arnaud-29-31 » 12 Sep 2012, 20:18
Tu traines des trucs inutiles dans ton calcul par exemple
)
ca doit être systématique ca se transforme en
)
.
Tu transformes le
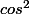
pour faire apparaitre du
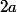
et

ce n'est vraiment pas judicieux puisqu'à terme on veut faire apparaître des simplifications. De plus tu traines un

sous le
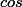
.
-
Shadoww
- Membre Naturel
- Messages: 14
- Enregistré le: 12 Sep 2012, 14:59
-
 par Shadoww » 12 Sep 2012, 20:31
par Shadoww » 12 Sep 2012, 20:31
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 12 Sep 2012, 20:35
par Luc » 12 Sep 2012, 20:35
et sinon, géométriquement ça veut dire quoi?
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 12 Sep 2012, 20:37
par Arnaud-29-31 » 12 Sep 2012, 20:37
Oui c'est juste. C'est déjà plus simple et on voit très bien qu'en développant
)
, on va avoir des termes qui vont se simplifier.
-
Shadoww
- Membre Naturel
- Messages: 14
- Enregistré le: 12 Sep 2012, 14:59
-
 par Shadoww » 12 Sep 2012, 20:45
par Shadoww » 12 Sep 2012, 20:45
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 12 Sep 2012, 20:50
par Arnaud-29-31 » 12 Sep 2012, 20:50
Je t'ai déjà dis que développer ainsi le
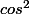
n'était pas judicieux, plus rien ne pourra se simplifier si tu fais apparaître dans
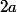
et

.
Tu avais deux fois
)
dans l'expression, pourquoi tu ne développe qu'un sur les 2 ?
-
Shadoww
- Membre Naturel
- Messages: 14
- Enregistré le: 12 Sep 2012, 14:59
-
 par Shadoww » 12 Sep 2012, 21:04
par Shadoww » 12 Sep 2012, 21:04
Merci de votre patience :happy2:
Vais reprendre à partir de là, car je ne vois pas comment faire autrement que développer le cos(a+b) au carré =X
^2+cos(b)^2+cos(a+b)^2-2(cos(a)cos(b)cos(a)cos(b) - cos(a)cos(b)sin(a)sin(b)) =)
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 12 Sep 2012, 21:05
par Arnaud-29-31 » 12 Sep 2012, 21:05
Bein de la meme manière que l'autre
)
, tu sais que
 = cosacosb - sinasinb)
-
Shadoww
- Membre Naturel
- Messages: 14
- Enregistré le: 12 Sep 2012, 14:59
-
 par Shadoww » 12 Sep 2012, 21:07
par Shadoww » 12 Sep 2012, 21:07
^2+cos(b)^2+[cos(a)cos(b)-sin(a)sin(b)]^2-2(cos(a)cos(b)cos(a)cos(b) - cos(a)cos(b)sin(a)sin(b)) =)
^2+cos(b)^2+[cos(a)cos(b)-sin(a)sin(b)]^2-2(cos(a)^2cos(b)^2 - cos(a)cos(b)sin(a)sin(b)) =)
^2+cos(b)^2+[cos(a)cos(b)-sin(a)sin(b)]^2-2cos(a)^2cos(b)^2 +2 cos(a)cos(b)sin(a)sin(b) =)
Mais après... =X A part développer les carrés =X
En utilisant
sin(b)=1/2 * (sin(a+b)+(sin(a-b)))
? =X
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 12 Sep 2012, 21:33
par Arnaud-29-31 » 12 Sep 2012, 21:33
Tu ne vois pas les simplifications qui apparaissent en développant le carré ?
Ce que tu proposes fais revenir en arrière, ca refait apparaitre des choses que l'on a pas donc qu'on ne pourra pas simplifier ni grouper avec d'autres termes.
Pour résumé pour l'instant on a :

avec
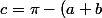)
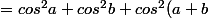 - 2.cosa.cosb.cos(a+b)))
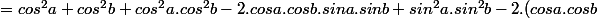.(cosa.cosb - sina.sinb))
Y'a vraiment beaucoup de simplification qui apparaissent arrivé là.
-
Shadoww
- Membre Naturel
- Messages: 14
- Enregistré le: 12 Sep 2012, 14:59
-
 par Shadoww » 12 Sep 2012, 21:45
par Shadoww » 12 Sep 2012, 21:45
Arnaud-29-31 a écrit:Tu ne vois pas les simplifications qui apparaissent en développant le carré ?
Ce que tu proposes fais revenir en arrière, ca refait apparaitre des choses que l'on a pas donc qu'on ne pourra pas simplifier ni grouper avec d'autres termes.
Pour résumé pour l'instant on a :

avec
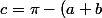)
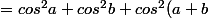 - 2.cosa.cosb.cos(a+b)))
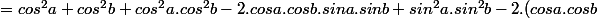.(cosa.cosb - sina.sinb))
Y'a vraiment beaucoup de simplification qui apparaissent arrivé là.
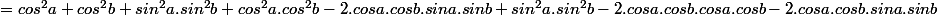
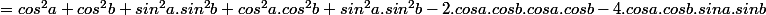
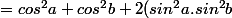-cosa.cosb.cosa.cosb - 4.cosa.cosb.sina.sinb)
[/TEX]
A chaque fois que je fais quoi que ce soit, ici, je retourne en arriere, les seules identités que je vois clairement, sont celles qui viennent d'etre développées =(
Les carrés doivent se simplifier pour doner le "1" de l'autre coté, mais... Les seuls que j'ai sont les cos qui sont additionnés et les sin qui sont multipliés oO

doit se simplifier, je cherche la formule mais...
Une bonne nuit de sommeil pour mediter sur ca et je vois ca demain, la tete fraîche et reposée =) Merci encore pour ce debut :+:
:id: de derniere minute : sin(2a) mais ca sent l'erreur :
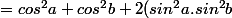 - cos^2a.cos^2b - sin(2b)sin(2a))
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 12 Sep 2012, 21:53
par Arnaud-29-31 » 12 Sep 2012, 21:53
Non, encore une fois pourquoi utiliser une formule qui rend plus compliquée l'expression.
La des simplifications sautent aux yeux, par exemple dans ma dernière ligne :
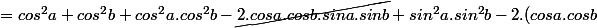.(cosa.cosb - \cancel{sina.sinb}))
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 70 invités
