F^-1 de x + cosh (x)

par **kutters_paradis** » 26 Juin 2008, 21:38

bonjour à tous je suis nouveau sur le forum et j'ai un petit problème pour vous :
la fonction est définie :

f(x) = x + cosh (x)

f^-1(x) = ? :marteau:

Avez vous la solution, moi non mais j'aimerais bien?

Merci

par **tize** » 27 Juin 2008, 08:29

Bonjour,
elle n'est même pas bijective...

par **mathelot** » 27 Juin 2008, 09:12

On peut essayer de l'inverser sur

. Le problème c'est de lier les parties paires et impaires de

à celles de f.

par **tize** » 27 Juin 2008, 10:33

Inverser la fonction sur R+ revient à résoudre

avec y>0 ce qui est impossible de manière algébrique me semble-t-il...

par **mathelot** » 27 Juin 2008, 16:56

re,
la fonction réciproque g vérifie:

, ce qui permettrait de chercher un DSE au voisinage de

encore faut-il calculer ses coeff et son rayon de convergence.

sinon, une autre possibilité:
comme la dérivation de f est périodique à cause du ch et qu'il y a une formule donnant la dérivée nième de g en fonction des dérivées successives de f, on arriverait peut être à "reconstituer" g par sa série de Taylor
en y=1, sans avoir l'assurance que la formule est valide sur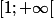

Noter que f est homomorphe, g aussi (à démontrer) et principe du prolongement analytique ?

F^-1 de x + cosh (x)

f^-1 de x + cosh (x)

Qui est en ligne