Corps Fp: trouver facilement les inverses d'une fraction

[yoshi13]

Bonjour à tous,

Je perds beaucoup de temps à trouver les inverses de fractions dans Fp, par exemple:

que vaut -1/2 dans F5? Ou 1/3 dans F11?

Je suis sûr qu'il y a des techniques mais lesquelles?

Merci d'avance

[zygomatique]

salut

théorème de Bachet-Bezout ...

2 * 3 = 1 [5]

3 * 4 = 1 [11]

[Ben314]

Salut,
Ainsi que l'algorithme d'Euclide étendu qui permet de déterminer très rapidement un et un tels que 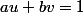du théorème sus mentionné.

Exemple : Déterminer l'inverse de 12 dans F_101
101/128 => 101 - 8x12 = 5
12/52 => 12 - 2x5 = 2 et en "remontant", 2 = 12 - 2x(101 - 8x12) = 17x12 - 2x101
5/22 => 5 - 2x2 = 1 et en "remontant", 1 = (101 - 8x12) - 2x(17x12 - 2x101) = 5x101 - 42x12
Donc l'inverse de 12 dans F_101 est -42 soit encore 101-42=59.

Y'a même moyen de le rédiger différemment vu que les coeff. qui apparaissent devant le 101 on s'en fout.
Mettons que tu ait à calculer A=-37/18 dans F_101. Tu écrit que

101/186 =>
18/73 =>
7/32 =>

Le tout, c'est de comprendre que c'est l'algorithme d'Euclide qui "pilote" les calculs (et à la limite de comprendre que dans l'algo. en question, c'est plus rapide de prendre l'entier le plus proche de a/b plutôt que le quotient de la division euclidienne de a par b, c'est à dire la partie entière de a/b)
Et tant que n'a pas plus de 3 ou 4 chiffres, ça se fait très bien à la main (rarement plus de 4 ou 5 itérations) et évidement, c'est "finger in the noze" avec une calculette programmable y compris pour des ayant 10 chiffres (au delà, la calculette risque de ne plus représenter les entiers de façon exacte et c'est évidement la cata.)

[yoshi13]

Hello,

merci pour vos réponses, j ai pu m entrainer un peu grâce à vos conseils et ca va beaucoup mieux

Bonne soirée