Bonjour,
je ne comprend rien au calcul qu'on effectue dans Fn[X]
par exemple pour explicité les polynome irreductible de degres 1 et 2 dans F2[X]
je pensais que c'etait X+1 et X²+1
et la reponse est X, X+1 et X²+X+1
?
donc X n'a pas de racine ? X=0 ?
et pourquoi X²+1 n'est pas irreductible ? quelle est sa racine ?
quelqun pourrais m'expliquer ?
Corps finis
5 messages
- Page 1 sur 1
Re: corps finis
Je laisse le soin aux spécialistes de corriger l'énoncé, les réponses et faire une explication dans les normes.
Re: corps finis
Salut,
Rappel : soit K un corps et P un polynôme de K[X]. On dit que P est irréductible sur K si :
- P n'est pas inversible (autrement dit, P n'est pas dans K*)
- pour tout Q,R dans K[X], si P=QR, alors Q ou R est inversible.
Autrement dit, tu ne peux pas écrire P comme produit de deux polynômes non inversibles tous les deux (remarque qu'on peut toujours écrire P comme le produit avec
avec  )
)
Ensuite,
proposition : soit K un corps et P dans K[X] un polynôme de degré 2 ou 3.
Alors P est irréductible dans K[X] si et seulement si P n'a pas de racine dans K.
Je t'encourage vraiment à démontrer cette proposition en revenant à la définition d'irréductibilité.
Donc déjà, cette proposition que tu sembles vouloir utiliser n'est valable que pour les polynômes de degré 2 ou 3 donc ne s'applique pas à X, de degré 1, qui est bien irréductible. Il suffit de revenir à la définition pour le montrer.
Déjà, il est clair que X n'est pas inversible.
Ensuite, si tu écris X = Q R avec Q,R dans K[X]\{0}, alors en passant aux degrés, on a : deq(QR)= deg(Q)+deg(R)=deg(X)=1 (cette égalité de degré est valable puisqu'on est dans un corps donc dans un anneau intègre).
On a alors,deg(R)) \in \{ (0,1);(1;0) \}) et donc forcément un des polynômes est constant (i.e dans K* donc inversible).
et donc forcément un des polynômes est constant (i.e dans K* donc inversible).
Donc par définition, X est irréductible dans K[X].
Enfin, X²+1 a bien une racine dans Z/2Z [X], c'est 1 :
1²+1=2=0 dans Z/2Z.
Rappel : soit K un corps et P un polynôme de K[X]. On dit que P est irréductible sur K si :
- P n'est pas inversible (autrement dit, P n'est pas dans K*)
- pour tout Q,R dans K[X], si P=QR, alors Q ou R est inversible.
Autrement dit, tu ne peux pas écrire P comme produit de deux polynômes non inversibles tous les deux (remarque qu'on peut toujours écrire P comme le produit
Ensuite,
proposition : soit K un corps et P dans K[X] un polynôme de degré 2 ou 3.
Alors P est irréductible dans K[X] si et seulement si P n'a pas de racine dans K.
Je t'encourage vraiment à démontrer cette proposition en revenant à la définition d'irréductibilité.
Donc déjà, cette proposition que tu sembles vouloir utiliser n'est valable que pour les polynômes de degré 2 ou 3 donc ne s'applique pas à X, de degré 1, qui est bien irréductible. Il suffit de revenir à la définition pour le montrer.
Déjà, il est clair que X n'est pas inversible.
Ensuite, si tu écris X = Q R avec Q,R dans K[X]\{0}, alors en passant aux degrés, on a : deq(QR)= deg(Q)+deg(R)=deg(X)=1 (cette égalité de degré est valable puisqu'on est dans un corps donc dans un anneau intègre).
On a alors
Donc par définition, X est irréductible dans K[X].
Enfin, X²+1 a bien une racine dans Z/2Z [X], c'est 1 :
1²+1=2=0 dans Z/2Z.
Modifié en dernier par Elias le 30 Mai 2018, 18:40, modifié 2 fois.
Pseudo modifié : anciennement Trident2.
Re: corps finis
Bonjour,
Revois la définition d'un polynôme irréductible, il n'y est pas question de racines : un polynôme est irréductible s'il n'est pas inversible et si ses diviseurs sont soit inversibles, soit le produit du polynôme lui-même par un inversible. Si tes coefficients sont dans un corps (i.e. pas juste un anneau), il en découle que tous les polynômes de degré 1 sont irréductibles.
Dans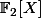 ,
, ^2) n'est pas irréductible, et il a 1 comme racine double. Et pour insister sur la différence entre être irréductible et ne pas avoir de racines, dans
n'est pas irréductible, et il a 1 comme racine double. Et pour insister sur la différence entre être irréductible et ne pas avoir de racines, dans 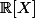 ,
, (X^2+\sqrt{2}X+1)) n'est pas irréductible, pourtant il n'a aucune racine.
n'est pas irréductible, pourtant il n'a aucune racine.
Revois la définition d'un polynôme irréductible, il n'y est pas question de racines : un polynôme est irréductible s'il n'est pas inversible et si ses diviseurs sont soit inversibles, soit le produit du polynôme lui-même par un inversible. Si tes coefficients sont dans un corps (i.e. pas juste un anneau), il en découle que tous les polynômes de degré 1 sont irréductibles.
Dans
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
