Corps engendré par une partie !

[barbu23]

Merçi yos !

[barbu23]

ça veut dire quoi ce terme : " à isomorphisme près " ?!
merçi d'avance !!

[barbu23]

Comment montrer qu'un corps fini est toujours de cardinal de la forme avec : premier.
et merçi infiniment !!

[kazeriahm]

On a le théorème suivant:
Soit un corps fini.
Soit le corps premier de .
Si , alors: alors est une puissance de la caractéristique de .
Voiçi la démonstration du théorème:
est un espace vectoriel.
Si : alors: .

salut, avec ce théorème tu as bien que card K =p^n isn't it ?

on dit que deux groupes (ou anneau, corps, ev, algebre,...) sont égaux à isomorphisme près s'il existe un isomorphisme de l'un dans l'autre

par exemple si j'ai bien compris les messages postés ci avant, en caracteristique 0, le sous corps premier d'un corps K est Q, à isomorphisme près

[barbu23]

Ohh ce que je suis con ..!! lol

[barbu23]

Bonsoir:
Quelqu'un pourrait m'expliquer ce qu'on entend par extension normale ..
et merçi infiniment !!

[yos]

Salut.
Je ferai pas mieux que ton cours : L est une extension normale d'un corps K lorsque L est le corps des racines d'un polynôme de K[X] (le corps obtenu en ajoutant à K toutes les racines d'un polynôme à coefs ds K).

Par exemple est une extension normale de Q car on l'obtient en lui ajoutant les racines de X²-2. mais n'est pas une extension normale de Q car le polynôme minimal de 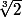est 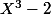et le corps ne contient pas les autres racines de ce polynôme.

[barbu23]

Bonjour:
Merçi yos pour ta dernière reponse !!
j'aimerai que vous me clarifier encore une fois, un truc que j'ai pas bien compris à propos de la définition du degré galoisien !!
Au départ, dans le cours, on donne la définition du degré galoisien, comme étant le cardinal de l'ensemble des isomorphismes de l'extension de dans une clôture normale de , et on le note comme ça : . après, on donne comme exemple celui çi: 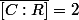, avec: : le corps des complexes et : le corps des réels.
Ma question est :
Pourriez vous me dire comme on aboutit à ce résultat qui est :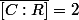 ..? . celà veut dire que le cardinal des isomorphismes de dans une clôture normale de est égale à .. mais je ne vois pas comment la démontrer .. quelle clôture normale choisir, et comment calculer ce résultat...
et merçi infiniment !!!

[kazeriahm]

les seuls automorphismes de corps de C sont l'identité et la conjugaison si je ne m'abuse

si ca peut t'aider...

[B_J]

les seuls automorphismes de corps de C sont l'identité et la conjugaison si je ne m'abuse

si ca peut t'aider...

... continus

[kazeriahm]

ah bon ?

en fait non ce sont les seuls automorphismes de corps de C tels que la restriction à R soit l'identité (je ne les suppose pas continus)

par ailleurs le seul automorphisme de corps de R est l'identité

[barbu23]

Comment on sait qu'ils sont les seuls automorphismes qui existent ... et merçi infiniment !!

[kazeriahm]

c'est les seuls automorphimes qui vérifient ...

il suffit de regarder l'image de i par de telles applications (f(i^2)=f(-1)=-1=f(i)^2 donc f(i)=i ou -i, et comme f(1)=1 par hypothese, on en déduit f(a+ib)=f(a)+if(b) ou -if(b)=a+ib ou a-ib

[barbu23]

Kazeriahm, tu peux me dire pourquoi : -1 = (f(i))^2 ... et merçi d'avance !!!

[barbu23]

la question est adréssée à tout le monde en fait ... il paraît que "kazeriahm" n'est pas là !!

[nuage]

Salut,
On a d'une part :
car la restriction de à est l'identité
Et d'autre part :
car est un morphisme.

[barbu23]

Ah oui c'est vrai, c'est un morphisme, j'ai oublié, je croyais qu'on parle uniquement en langage d'espaces vectoriels et matrices ... !! merçi , nuage !!!