Corps algebriquement clos

[barbu23]

Bonjour à tous, :happy3:
Pourriez vous m'expliquer pourquoi un corps algébriquement clos, peut ne pas être une clôture algébrique ?
Merci d'avance. :happy3:

[barbu23]

Un petit up pour voir si quelqu'un a une réponse. :happy3:
Merci d'avance. :happy3:

[Losange]

Considérons trois corps distincts : , 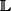et 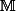tels que :

• 
• et sont algébriquement clos.

Il est clair que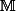 est algébriquement clos et contient mais n'est pas la clôture algébrique de .

On peut prendre par exemple :

• 
• est le corps des complexes algébriques, c'est-à-dire des complexes qui sont solution d'un polynôme à coefficients entiers.
• 

[barbu23]

Je n'ai pas compris, quelle est la différence entre un corps qui est algébriquement clos et une clôture algébrique ?
Je n'ai pas les bonnes définition, pouvez vous me rappeler les définitions que vous utilisez ?
Merci d'avance.

[L.A.]

Bonsoir.

Une clôture algébrique d'un corps fixé K est une extension algébrique L/K avec L est un corps algébriquement clos (c'est à dire sur lequel tout polynôme non constant est scindé en facteurs de degré 1).

Comme l'a dit Losange, si tu prends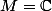 et 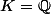alors M est algébriquement clos (théorème de Gauss-d'Alembert bien connu) mais n'est pas algébrique sur K ( est transcendant par exemple) donc M/K n'est pas une clôture algébrique.

[alavacommejetepousse]

Bonjour à tous, :happy3:
Pourriez vous m'expliquer pourquoi un corps algébriquement clos, peut ne pas être une clôture algébrique ?
Merci d'avance. :happy3:

bonjour dit comme ça c'est faux:
toute clôture algébrique est algébriquement close !
et
tout corps algébriquement clos est une clôture algébrique : la sienne!

en revanche comme dit plus haut tout corps algébriquement clos n'est pas nécessairement la clôture algébrique d'un sous corps DONNE