Coordonnées point d'étude

[cedricdef]

Bonsoir,

Pouvez-vous m'aider à trouver les coordonnées d'un point O que j'ai analysé (pour la facilité, imaginez un triangle fait par les points de référence et le point O se trouve dans ce triangle)? Pour ce faire, je connais les angles depuis ce point O vers les trois points de référence dont on connaît les coordonnées;

A x=167601,760700 y=152222,611700
C x=167510,304400 y=152351,394200
D x=167549,606900 y=152434,967800

Si on fixe 0 degrés comme étant l'axe O-D, le point A se trouve sur l'axe à 133.65 degrés et le point C sur l'axe à 324 degrés (à chaque fois l'angle est mesuré depuis le point O).

Intuitivement, je pense qu'un seul point satisfait à ces critères et j'en cherche donc les coordonnées.

Merci beaucoup d'avance,

Cédric

[hdci]

Bonjour,

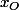Je pense que je traiterais ainsi : je commence par faire un changement de repère pour mettre O au centre du repère (une simple translation), donc A a pour coordonnée etc., où et 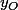sont les inconnues.

Puis je considèrerais les deux rotations vectorielles d'angle 133,65° et 324° : j'obtiendrais ainsi deux matrices avec les cosinus et sinus de ces angles.

Alros le vecteur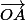 est colinéaire au vecteur image de 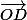par la première rotation, et de même pour 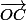avec la seconde rotation. Soient et les deux coefficients de colinéarité (ou les deux rapports d'homothétie)
Tout ceci me donnerait un système de 4 équations à 4 inconnues () "qu'il n'y a plus qu'à résoudre".

Je mets les guillemets car le système n'est pas linéaire, donc pas forcément très pratique à résoudre

[fatal_error]

yo,

dans l'approche ci-dessous par exemple, j'itère sur le point M qu'on cherche, (tq angle(MD,MA)=133 et angle(MD,MC) = 324) et je regarde en calculant justement la rotation de de centre M du point D, si il se retrouve aligné avec [MD,MA)

Code: Tout sélectionner

1;
clear all;
global A=[167601.760700,152222.611700]';
global C=[167510.304400,152351.394200]';
global D=[167549.606900,152434.967800]';
global angleA = 133.65 * pi/180
global angleC = 324 * pi/180
function r = myangle(M,F,G)
    xM = M(1);
    yM = M(2);
    xF = F(1);
    yF = F(2);
    xG = G(1);
    yG = G(2);
    vMF = [xF-xM, yF-yM];
    vMG = [xG-xM, yG-yM];
    r = mod(atan2( (vMF(1)*vMG(2)) - (vMG(1)*vMF(2)), vMF*vMG')+2*pi, 2*pi);
endfunction


function res = angleAlign(M,D,A, a)
    Dm = D-M;
    Ap = [Dm(1)*cos(a)-Dm(2)*sin(a), Dm(1)*sin(a)+Dm(2)*cos(a)]' + M;
    MA = A-M;
    MAp = Ap-M;
    res = (1- (MA'*MAp)/(norm(MA)*norm(MAp)))^2;

endfunction
function res = phi (M)
    global A;
    global C;
    global D;
    global angleA;
    global angleC;

    res = angleAlign(M, D, A, angleA)+angleAlign(M,D,C, angleC);
    return;
endfunction


I=(A+C+D)/3;
[x, obj, info, iter, nf, lambda]=sqp(I,@phi)


angleMDA = (myangle(x,D,A))*180/pi
angleMDC = (myangle(x,D,C))*180/pi


resultat:

Code: Tout sélectionner

x =

   1.6760e+05
   1.5222e+05

obj =  0.21523
info =  104
iter =  28
nf =  88
lambda = [](0x1)
angleMDA =  133.99
angleMDC =  21.583



on voit que l'angle (MD,MC) trouvé est loin d'être satisfaisant.

Peut-être qu'il y a des problèmes dans ma modélisation (à cause des prob numériques??), j'ai aussi tenté une approche avec pour erreur l'écart aux angles attendus, qui ne donne pas non plus un résultat satisfaisant

Code: Tout sélectionner

1;

global A=[167601.760700,152222.611700];
global C=[167510.304400,152351.394200];
global D=[167549.606900,152434.967800];
global tana = mod((133.65 * pi/180)+2*pi, 2*pi)
global tanb = mod((324 * pi/180)+2*pi, 2*pi)
tana
tanb
function r = myangle(M,F,G)
    xM = M(1);
    yM = M(2);
    xF = F(1);
    yF = F(2);
    xG = G(1);
    yG = G(2);
    vMF = [xF-xM, yF-yM];
    vMG = [xG-xM, yG-yM];
    r = mod(atan2( (vMF(1)*vMG(2)) - (vMG(1)*vMF(2)), vMF*vMG')+2*pi, 2*pi);
endfunction
function res = phi (M)
    global A;
    global C;
    global D;
    global tana;
    global tanb;

    %(OD,OA)
    tanu = myangle(M, D, A);
    tanv = myangle(M, D, C);
    res = (tanu - tana)^2 +(tanv-tanb)^2;
    res = abs(tanu - tana) + abs(tanv - tanb);
    return;
endfunction


I=(A+C+D)/3;
tana
[x, obj, info, iter, nf, lambda]=sqp(I,@phi)


angleMDA = (myangle(x,D,A))*180/pi
angleMDC = (myangle(x,D,C))
angleCDA = myangle(C,D,A)*180/pi


Code: Tout sélectionner

tana =  2.3326
tanb =  5.6549
tana =  2.3326
x =

   1.6759e+05
   1.5240e+05

obj =  4.4239
info =  104
iter =  12
nf =  52
lambda = [](0x1)
angleMDA =  133.65
angleMDC =  1.2310


comme on constate que tout le temps le premier angle est correct, vu que je suis un boucher, la prochaine étape est probablement de se poser en A (par ex) et d'itérer avec des rayons R de plus en plus grand et pour un R donné, de calculer d'abord l'unique point M respectant l'angle (MD,MA), puis pour ce point M, de calculer l'angle (MD,MC) et de (1 regarder comment l'angle évolue parce que je vois rien, et 2 garder le meilleur angle)

[fatal_error]

edit: on ne peut plus supprimer de message

[cedricdef]

merci beaucoup à vous! au final j'ai trouvé une autre façon de faire avec les notions d'arc capable et les intersections entre les deux cercles ainsi créés, mais vos approches me paraissent bien plus simples !

[fatal_error]

pour information trouves-tu une solution avec les valeurs que tu as fournies? (si oui laquelle?)

[GaBuZoMeu]

Les informations transmises sont erronées : aucun point n'y correspond, puisque les arcs capables ne s'intersectent pas :

[GaBuZoMeu]

Si par hasard les mesures d'angles sont données à la façon de la topométrie, dans le sens horaire, alors les arcs capables sont les symétriques des précédents. Ils sont ici représentés en bleu, et s'intersectent au point de coordonnées (-69.52, 87.66) dans le repère ayant A comme origine, ce qui fait (167532.14, 152318.17) dans le repère d'origine.
Après, il y a peut-être d'autres choses que cedricdef ne nous a pas dites, concernant les coordonnées. Ce ne sont peut-être pas des coordonnées dans un repère orthonormé pour une unité de longueur inconnue.
Toutes choses à préciser quand on veut bien poser son problème.

[fatal_error]

merci GaBuZoMeu pour la notion d'arcs capables!
et bien vu pour les angles à prendre dans l'autre sens....

je parviens de fait bien à la solution avec le code suivant:

Code: Tout sélectionner

1;

global A=[167601.760700,152222.611700];
global C=[167510.304400,152351.394200];
global D=[167549.606900,152434.967800];
global tana = mod((-133.65 * pi/180)+2*pi, 2*pi)
global tanb = mod((-324 * pi/180)+2*pi, 2*pi)
tana*180/pi
tanb*180/pi
function r = myangle(M,F,G)
    xM = M(1);
    yM = M(2);
    xF = F(1);
    yF = F(2);
    xG = G(1);
    yG = G(2);
    vMF = [xF-xM, yF-yM];
    vMG = [xG-xM, yG-yM];
    r = mod(atan2( (vMF(1)*vMG(2)) - (vMG(1)*vMF(2)), vMF*vMG')+2*pi, 2*pi);
endfunction
function res = phi (M)
    global A;
    global C;
    global D;
    global tana;
    global tanb;

    %(OD,OA)
    tanu = myangle(M, D, A);
    tanv = myangle(M, D, C);
    res = (tanu - tana)^2 +(tanv-tanb)^2;
    %res = abs(tanu - tana) + abs(tanv - tanb);
    return;
endfunction


I=(A+C+D)/3;
[x, obj, info, iter, nf, lambda]=sqp(I,@phi);

M=x
angleMDA = (myangle(x,D,A))*180/pi
angleMDC = (myangle(x,D,C))*180/pi

%with established solution
%tanu = myangle([167532.14, 152318.17], D, A)*180/pi
%tanv = myangle([167532.14, 152318.17], D, C)*180/pi





d'une manière assez intéressante la minimisation de l'objectif res = abs(tanu - tana) + abs(tanv - tanb); ne donne pas le point M escompté alors que les carrés oui