Coordonné d'une point

par **ccsabry** » 26 Mai 2014, 23:52

mon problème est le suivant : 3 points A,B et C j'ai les coordonnés (x,y) de B et C et la distance entre A et B "d1" et la distance entre A et C "d2" est ce qu'il est possible de connaitre les coordonnés de la point A :help: :help: :help:

par **Robic** » 27 Mai 2014, 00:57

Houlà, ton message est à la limite de la lisibilité (faute de ponctuation). Quoiqu'il en soit, la réponse est oui. D'ailleurs ça se voit en faisant un dessin : tu peux placer B et C avec leurs coordonnées, et ensuite tu reportes au compas les distances AB et AC pour placer A. Ce qui, au passage, te fournit la méthode pour calculer les coordonnées de A.

par **ccsabry** » 27 Mai 2014, 01:47

j'ai une travail de mémoire sur Microsoft kinect , alors j'ai les coordonnés de deux Points par exemple B(1,4) et c(3,2) et j'ai la distance(AB)=3 et la distance (AC) =2 ; j'aime avoir une formule qui peut déduire les coordonnés de la point A

Merci

par **chan79** » 27 Mai 2014, 06:05

ccsabry a écrit:j'ai une travail de mémoire sur Microsoft kinect , alors j'ai les coordonnés de deux Points par exemple B(1,4) et c(3,2) et j'ai la distance(AB)=3 et la distance (AC) =2 ; j'aime avoir une formule qui peut déduire les coordonnés de la point A

Merci

Bonjour
Tu as tout ce qu'il ce qu'il faut pour écrire l'équation du cercle de centre B et de rayon 3 ainsi que l'équation du cercle de centre C et de rayon 2. Tu dois résoudre le système. le système.
Ca te donne deux points A et A'.

par **Robic** » 27 Mai 2014, 06:30

Quand on fait le dessin, on voit qu'il faut dessiner deux cercles et que le point cherché est leur intersection.

Si le but est de trouver une formule, voyons ça sur ton exemple : B(1,4), C(3,2), AB=3 et AC=2. On note (x,y) les coordonnées de A, puis on écrit les hypothèses en fonction de x,y :

AB = 3 AB² = 9 (x-1)² + (y-4)² = 9 (1)
AC = 2 AC² = 4 (x-3)² + (y-2)² = 4 (2)

(1) et (2) sont en fait les équations des cercles dont parle Chan79.

Ce système n'est pas facile à résoudre. On peut par exemple procéder ainsi :
(1) (y-4)² = 9 - (x-1)²

ou

. Il y a deux valeurs possibles de y (normal, il y aura deux points, comme indiqué par Chan79), et on reporte chacun de ces deux choix dans l'équation (2). Avec la première valeur, par exemple, ça donnera :

, d'où on en déduit (y-2)² en fonction de x, et ainsi il n'y a plus que des x dans l'équation (2). Mais (2) devient drôlement compliquée, avec toutes ces racines carrées...

En fait, j'ai bien peur qu'il n'y ait pas de formule simple. Par contre on peut facilement écrire un algorithme (qui permettra de calculer des valeurs décimales à l'ordinateur) à partir du raisonnement ci-dessus.

par **chan79** » 27 Mai 2014, 06:41

Salut Robic
J'arrive à l'équation du second degré 32x²-168x+161=0 (ligne (1) - ligne (2) pour obtenir 4x-4y=1)

et

On peut généraliser pour des coordonnées de B et C quelconques et des distances quelconques. Et on a les coordonnées de A et A' si ces points existent. Il y aura des cas particuliers à examiner.

par **Robic** » 27 Mai 2014, 07:44

Ah oui, c'est plus judicieux que ce que j'avais commencé, donc on doit en effet pouvoir obtenir une formule générale. Du moins à condition que les points A et A' existent (pour ça il faut que AB+AC soit supérieur ou égal à BC).

par **Tiruxa** » 27 Mai 2014, 09:40

Bonjour une autre méthode possible en utilisant les angles.

Pas d'équation à résoudre mais utilisation d'un arc cos et donc résultat en valeur approchée.

Le principe on calcule l'angle

par le th d'Al Khashi

Dans l'exemple on obtient

Ensuite écrire les coordonnées polaires du vecteur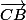

puis du vect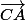eur

On trouve

D'où les coordonnées polaires du vecteur

d'où les coordonnées cartésiennes de A

On retrouve les valeurs approchées des solutions exactes donnéees par chan79.

par **ccsabry** » 27 Mai 2014, 09:51

Bonjour, Merci pour votre réponse mais pourquoi il doit avoir 2 points A et A' , ici les deux droites AB et AC ses coupes en points A
j'ai donné des valeurs arbitraires mais mon problème provient de mon sujet de Mémoire je travaille avec Microsoft Kinect qui peut déterminer les coordonnés des joints d'une personne ainsi la distance entre elle et ces joints ,supposant qu'on a deux joints "shoulder" (s) et "elbow" (e) avec S(x1,y1) et e(x2,y2) et la distance kinect-shoulder et kinect-elbow sont tous des valeurs connues ,il reste ici à déterminer la position de "Kinect"(K) K(x,y) dont le but de calculer l'angle SKE

par **chan79** » 27 Mai 2014, 11:00

ccsabry a écrit:Bonjour, Merci pour votre réponse mais pourquoi il doit avoir 2 points A et A' , ici les deux droites AB et AC ses coupes en points A
j'ai donné des valeurs arbitraires mais mon problème provient de mon sujet de Mémoire je travaille avec Microsoft Kinect qui peut déterminer les coordonnés des joints d'une personne ainsi la distance entre elle et ces joints ,supposant qu'on a deux joints "shoulder" (s) et "elbow" (e) avec S(x1,y1) et e(x2,y2) et la distance kinect-shoulder et kinect-elbow sont tous des valeurs connues ,il reste ici à déterminer la position de "Kinect"(K) K(x,y) dont le but de calculer l'angle SKE

Pour l'angle

, le théorème d'Al Kashi te donne directement la réponse:

par **ccsabry** » 27 Mai 2014, 11:18

Merci infiniment chan79 , je cherche cette formule depuis deux jours, je continuerai mon travail de mémoire grace à vous
Merci encore :ptdr: :ptdr: :ptdr: :ptdr:

par **deltab** » 02 Juin 2014, 20:39

Bonsoir.

@ccsabry
Le problème tel que tu l'as posé revient bien à l'intersection de 2 cercles centrés en B et C. Comme le point que tu cherches, tu le prends dans un des demi-plans délimités par la droite BC, il est alors unique. Si l'on veut faire de la reconnaissance faciale, on se place devant le sujet en non derrière

Coordonné d'une point

Coordonné d'une point

Qui est en ligne