Convexité et projection
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
GagaMaths
- Membre Relatif
- Messages: 316
- Enregistré le: 29 Oct 2011, 13:28
-
 par GagaMaths » 11 Nov 2011, 12:32
par GagaMaths » 11 Nov 2011, 12:32
Bonjour!
Je bloque sur un exercice d'entraînement , voici l'énoncé :
Soit K un cône convexe fermé de R^n et K0 = { y R^n, <= 1 pour tout x K }
<.,.> est le produit scalaire euclidien.
1) Vérifier que que K0 = { y R^n, <= 0 pour tout x K }
2) On note Pk(x) la projection de x R^n sur K. Montrer que l'application Pk vérifie les propriétés suivantes :
pour tout x de R^n, pour tout t > O, Pk(tx) = tPk(x)
pour tout x de R^n, ||x||² = ||Pk(x)||²+||x-Pk(x)||²
3) Montrer l'équivalence entre :
(i) x = y+z où y K, z K0 et = 0
(ii) y = Pk(x) et z= Pk0(x)
1) Si j'appelle A l'ensemble { y R^n, <= 0 pour tout x K }, je vois clairement que A c K0.
Par contre je ne vois pas comment montrer l'autre inclusion.
2) Comment écrire concrètement cette projection ?
Je ne sais pas si je dois utiliser la caractérisation de la projection ou bien dire que c'est l'inf des distances...
3) Idem...
Je cherche juste quelques indications pour bien partir, merci beaucoup !
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 11 Nov 2011, 13:20
par cuati » 11 Nov 2011, 13:20
Bonjour,
pour le 1)
suppose qu'il existe

et
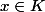
tel que
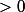
alors pour tout
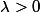
, on a

et que peut-on dire de

?
-
GagaMaths
- Membre Relatif
- Messages: 316
- Enregistré le: 29 Oct 2011, 13:28
-
 par GagaMaths » 11 Nov 2011, 13:25
par GagaMaths » 11 Nov 2011, 13:25
= lambda ?
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 11 Nov 2011, 13:29
par cuati » 11 Nov 2011, 13:29
Oui, et si

est assez grand ...
-
GagaMaths
- Membre Relatif
- Messages: 316
- Enregistré le: 29 Oct 2011, 13:28
-
 par GagaMaths » 11 Nov 2011, 13:34
par GagaMaths » 11 Nov 2011, 13:34
Pour lambda qui tend vers +oo, alors tend vers +oo
comme y K0, pour tout X dans K, on a <= 1
contradiction car lambda. x K
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 11 Nov 2011, 13:41
par cuati » 11 Nov 2011, 13:41
Ok,
donc l'hypothèse de départ : "'il existe

et
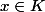
tel que

" est fausse... donc

pour tout

et

.
-
GagaMaths
- Membre Relatif
- Messages: 316
- Enregistré le: 29 Oct 2011, 13:28
-
 par GagaMaths » 11 Nov 2011, 13:43
par GagaMaths » 11 Nov 2011, 13:43
Ok merci j'ai compris cette question!
Maintenant pourrais-tu me donner des indications pr la question 2 ?
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 11 Nov 2011, 13:48
par cuati » 11 Nov 2011, 13:48
En général, dans un e.v.n. complet (ce qui est le cas ici puisque tu es en dimension finie), la projection d'un élément x sur une partie convexe fermée

s'écrit
)
et est définie par :
||=\inf\limits_{y\in K}||x-y||)
-
GagaMaths
- Membre Relatif
- Messages: 316
- Enregistré le: 29 Oct 2011, 13:28
-
 par GagaMaths » 11 Nov 2011, 13:52
par GagaMaths » 11 Nov 2011, 13:52
Ok mais alors là je considère quoi comme application Pk ?
du coup dans la question 2 je dois étudier cela :
||tx - Pk(tx) || = inf ||tx -y||
mais je ne vois pas quoi faire...
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 11 Nov 2011, 13:56
par cuati » 11 Nov 2011, 13:56
Oui, prends juste le terme de droite :
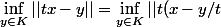||=t\inf\limits_{y\in K}||x-y/t||)
puis utilise le fait que K est un cône et donc

-
GagaMaths
- Membre Relatif
- Messages: 316
- Enregistré le: 29 Oct 2011, 13:28
-
 par GagaMaths » 11 Nov 2011, 14:01
par GagaMaths » 11 Nov 2011, 14:01
exact, donc quand j'aboutis à
||tx - Pk(tx) || = inf(tx-y) = t.inf(x -y/t)
y K, K est un cône, t>0 donc 1/t >0 donc y/t K.
si on note z= y/t
|| tx - Pk(tx) || = t . inf(x-z) = t || x - Pk(x) ||
donc là c'est bon pr cette partie ?
-
GagaMaths
- Membre Relatif
- Messages: 316
- Enregistré le: 29 Oct 2011, 13:28
-
 par GagaMaths » 11 Nov 2011, 14:04
par GagaMaths » 11 Nov 2011, 14:04
pour l'autre partie de la question, j'ai mis
||x||² = || x - Pk(x) + Pk(x) || ² puis après je devleoppe, cest une bonne idée ?
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 11 Nov 2011, 15:20
par cuati » 11 Nov 2011, 15:20
\in K)
qui est un cône donc pour tout
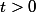
,
\in K)
et par définition de l'inf :
||^2\leq||x-tP_K(x)||^2=||x-P_K(tx)||^2)
ensuite développe à gauche et à droite...
-
GagaMaths
- Membre Relatif
- Messages: 316
- Enregistré le: 29 Oct 2011, 13:28
-
 par GagaMaths » 11 Nov 2011, 17:59
par GagaMaths » 11 Nov 2011, 17:59
je ne comprends pas trop l'inégalité....
sinon en developpant on obtient :
||x||² + ||Pk(x)||² - 2 <= ||x||² + ||Pk(tx)||² - 2
mais je n'ai plus de ||x||² après...
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 11 Nov 2011, 18:14
par cuati » 11 Nov 2011, 18:14
Oui, ensuite, si tu sors les "t" tu as un polynôme en "t" dont 1 est une racine évidente et dont tu connais le minimum qui est justement cette racine. C'est donc aussi une racine de la dérivée de ce polynôme...
-
GagaMaths
- Membre Relatif
- Messages: 316
- Enregistré le: 29 Oct 2011, 13:28
-
 par GagaMaths » 11 Nov 2011, 18:25
par GagaMaths » 11 Nov 2011, 18:25
oui j'obtiens donc :
||x||² + ||Pk(x)||² - 2 <= ||x||² + ||Pk(tx)||² - 2
||Pk(x)||² - 2 <= t²||Pk(x)||² - 2t
d'où : P(t) = t²||Pk(x)||² - 2t - ||Pk(x)||² + 2 >= 0
1 est racine du polynôme P.
par contre l'histoire du minimum je comprends pas bien...
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 11 Nov 2011, 18:35
par cuati » 11 Nov 2011, 18:35
Regarde mon message de 15h20, par définition de la projection, le minimum est atteint justement quand t=1.
Maintenant trace une fonction polynôme du second degré qui est positive et qui admet un zéro en t=1. La dérivée aussi s'annule donc en 1 donc :
 = 2t||Pk(x)||^2 - 2)
s'annule en t=1 i.e.
||^2=)
-
GagaMaths
- Membre Relatif
- Messages: 316
- Enregistré le: 29 Oct 2011, 13:28
-
 par GagaMaths » 11 Nov 2011, 18:48
par GagaMaths » 11 Nov 2011, 18:48
en fait ce que tu dis, c'est que j'ai :
P(t) >= 0 et P(1) = 0
donc nécessairement 1 est une racine double (c'est vrai que sur un dessin on voit que P ne s'annule pas ailleurs)...
par contre je n'ai pas bien compris l'inégalité avec x et tx je vois pas pq l'inf avec Pk(x) est inférieur à l'inf avec tPk(x) ...
j'ai essayé la question 3) mais je ne vois pas du tt comment faire !....
-
GagaMaths
- Membre Relatif
- Messages: 316
- Enregistré le: 29 Oct 2011, 13:28
-
 par GagaMaths » 12 Nov 2011, 19:07
par GagaMaths » 12 Nov 2011, 19:07
Je bloque sur la question 3 svp... !
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 13 Nov 2011, 20:06
par cuati » 13 Nov 2011, 20:06
Salut,
désolé de te répondre seulement maintenant mais j'ai eu d'autres trucs à faire...
Alors reprenons là où nous en étions :
=2t||P_K(x)||^2-2)
admet 1 comme racine, donc
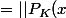||^2)
.
Maintenant, il suffit d'écrire :
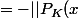||^2=0)
et du coup :
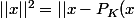+P_K(x)||^2=||x-P_K(x)||^2+||P_K(x)||^2+2 \underbrace{}_{= 0})
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 18 invités
