Convexité/concavité

[ck97]

Bonjour,
Je travaille actuellement sur un exercice portant sur les fonctions de deux variables. Il se décompose en 3 étapes :
-Calculer les dérivées partielles premières
-Expliciter la matrice hessienne
-Etudier la convexité/concavité de la fonction
Cependant je ne comprends pas cette dernière étape : comment je peux étudier la convexité/concavité d'une fonction à partir de sa matrice hessienne ?
Y a t-il une méthode particulière ?
Je vous remercie.

[aviateur]

Bonjour, si ta fonction est assez régulière
Est ce que tu peux écrire un développement de Taylor à l'ordre 2 en un point donné?
Le terme de la partie régulière d'ordre 2 est de la forme où h est l'accroissement
par rapport au pont donné.
Que se passe-t-il si H est s.d.p? si -H est s.d.p ? et dans les autres cas?
Tu devrais donner ton exemple et dire ce que tu as fait.

[Kolis]

Bonjour !
La convexité consistant à étudier le signe de pour sous-ensemble de 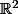où la fonction est définie, il n'est pas impossible que l'expression des en utilisant la hessienne soit utilisable.
Sans avoir ton énoncé complet je ne peux rien dire ...

[ck97]

soit la fonction f(x,y)= 4x^2-12xy+5y^2
-Calculer les dérivées partielles premières :
df/dx=8x-12y et df/dy=-12x+10y
-Expliciter la matrice hessienne:
je calcul les dérivées secondes => d^2f/dx^2=8 et d^2f/dy^2=10 et d^2f/dxdy=-12 et d^2f/dydx=-12
J'ai donc ma matrice hessienne :
8 -12
-12 10
-Etudier la convexité/concavité de f:
je pense devoir utiliser la matrice hessienne pour conclure sur cette dernière question ...

[aviateur]

Bonjour
Ici tu est dans la situation très particulière où f est un polynômes homogènes de degré 2. Donc tu peux déjà remarquer que H est une constante (la situation est la même en chaque point de R^2) et de plus
1/2 (h,k) H (h,k)=f(h,k).


La matrice H admet pour valeurs propres (tuppeux aussi travailler avec det(H) et la trace(H))
Elle est donc ni positive , ni négative. Si cela avait été le cas par exemple s.d.p
tu aurais eu localement une fonction convexe et donc globalement à cause d ma remarque.
La fonction ici est donc ni convexe ni concave. En chaque point tu as un point col.