Convexes

par **pHi** » 15 Mai 2006, 20:49

Bonjour :)

J'ai un petit probleme en analyse fonctionnelle.

Voici l'énoncé de mon exercice :

Soit G, l'ensemble des parties convexes compactes non vides B de A tq
si pour x,y dans A on a (1-t)x+ty appartient a B avec 0Montrer que G admet un élément minimal B. (Zorn)

Je pensais avoir compris la construction du G. Mais je voix absolument pas comment cet ensemble peut etre ordonné.

Je voudrais également savoir si on peut utiliser Zorn en le modifiant pour les minimum pour montrer directement que G admet bien un minimum. Zorn est utilisé pour les maximums normallement non ?

Merci d'avance :)

par **nuage** » 15 Mai 2006, 20:55

Salut,
sans aucune garantie : G est ordonné par l'inclusion et son minimum est la fermeture de l'intérieur de A.

par **abcd22** » 15 Mai 2006, 20:56

Bonsoir,
Ici je pense que ça marche en définissant comme ordre :

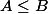
ssi

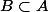
. Si on peut appliquer Zorn avec cet ordre on obtiendra un élément maximal pour cet ordre qui sera un élément minimal de G au sens de l'inclusion.

par **pHi** » 15 Mai 2006, 20:59

merci pour vos réponses si rapides je vais y refléchir encore :p
:mur:

par **nuage** » 15 Mai 2006, 21:04

Ma reponse précédente est fausse.

par **serge75** » 15 Mai 2006, 21:22

Peux-tu préciser ton énoncé :
est-ce il existe t dans ]0,1[ ou pour tout t dans ]0,1[ ?

par **pHi** » 16 Mai 2006, 06:09

j'ai donné l'énoncé que lon ma donné :)
je pense que c'est il existe un t

Convexes

Convexes

Qui est en ligne