Bonjour je bloque pour montrer la convergence uniforme d'une série ..
C'est la somme des : n² x^n
J'ai essayer de montrer la convergence normale de cette série en la majorant par la borne supp de son rayon de convergence (=1) mais je tombe sur n^2 et ça marche pas ducoup
Vous auriez des pistes svp ? je bloque
Merci d'avoir lu bonne journée
Convergence uniforme d'une série entiere
11 messages
- Page 1 sur 1
Re: Convergence uniforme d'une série entiere
GaBuZoMeu a écrit:Convergence uniforme sur quelle partie de?
Sur mon rayon de convergence donc sur ]-1,1[
Re: Convergence uniforme d'une série entiere
mathelot a écrit:j'ai calculé la série:
pour
J'ai aussi trouvé ça mais pour utiliser le théorème d’interversion dérivation somme il faut d'abord montrer la convergence uniforme
Re: Convergence uniforme d'une série entiere
On a la convergence uniforme sur tout intervalle compact [-r;r] où 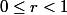
Re: Convergence uniforme d'une série entiere
On n'a pas convergence uniforme sur  , mais la propriété plus faible indiquée par mathelot. Plus faible, mais suffisante.
, mais la propriété plus faible indiquée par mathelot. Plus faible, mais suffisante.
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 16 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
