Convergence uniforme sur tout segment de R et sur R
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Beta
- Membre Naturel
- Messages: 41
- Enregistré le: 01 Mai 2019, 16:50
-
 par Beta » 25 Oct 2019, 15:29
par Beta » 25 Oct 2019, 15:29
Bonjour,
En travaillant sur les suites et séries de fonctions, je ne suis pas parvenu à comprendre pour quel raison :
"Ce n'est parce que
)
converge uniformément vers f sur tout segment [a,b] inclus dans

que
)
converge uniformément vers

sur

tout entier."
Pourriez vous m'expliquer ?
Respectueusement
Beta
-
Kolis
- Membre Relatif
- Messages: 482
- Enregistré le: 25 Sep 2015, 16:29
-
 par Kolis » 25 Oct 2019, 15:33
par Kolis » 25 Oct 2019, 15:33
Bonjour !
Il suffit de traduire chacune des notions que tu veux comparer :
Comment écris-tu la convergence uniforme sur tout segment ?
Comment écris-tu la convergence uniforme sur

?
Ou alors tu trouves des exemples :
La fonction exponentielle est limite uniforme de fonctions polynômes sur tout segment.
Est-ce encore vrai sur l'ensemble des réels ?
-
Beta
- Membre Naturel
- Messages: 41
- Enregistré le: 01 Mai 2019, 16:50
-
 par Beta » 25 Oct 2019, 15:53
par Beta » 25 Oct 2019, 15:53
Bonjour
Kolis,
La définition d'une convergence uniforme sur tout segment

de

(Resp

) est :
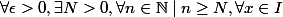
(Resp
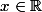
) ,
-f(x) \mid \leq \epsilon)
.
Sachant que

peut-être aussi grand que l'on veut, j'ai un peu de mal à voir en quoi ce n'est pas pareille.

-
jsvdb
- Membre Naturel
- Messages: 89
- Enregistré le: 20 Jan 2017, 09:45
-
 par jsvdb » 25 Oct 2019, 16:00
par jsvdb » 25 Oct 2019, 16:00
Juste une remarque : au sens de la distance usuelle, un segment peut être aussi grand que tu veux, il aura toujours une mesure finie à côté de celle IR
Bienheureux les fêlés car ils laissent passer la lumière !
-
Beta
- Membre Naturel
- Messages: 41
- Enregistré le: 01 Mai 2019, 16:50
-
 par Beta » 25 Oct 2019, 17:20
par Beta » 25 Oct 2019, 17:20
Merci vous deux,
je crois que j'ai finalement compris grâce à vous
-
Kolis
- Membre Relatif
- Messages: 482
- Enregistré le: 25 Sep 2015, 16:29
-
 par Kolis » 25 Oct 2019, 22:05
par Kolis » 25 Oct 2019, 22:05
Bonsoir !
Il faudrait écrire, en notant

l'ensemble des segments :
\in\N,\;\dots)
ce qui montre que

dépend à la fois de

et de

.
Maintenant pour trouver un

qui ne dépend pas de

, tu peux courir !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 77 invités