Convergence uniforme pour une fonction convergente
14 messages
- Page 1 sur 1
Convergence uniforme pour une fonction convergente
Bonsoir je bloque sur cette question j'aimerais quelques pistes
Soit f :R+->R et convergente et continue
f convergente , on apelle L sa limite , donc pour tout E >0 il existe x0>0 tq pour tout x >= x0 on a |f(x)- L|< E
On en déduit que |f(x)-f(y)|< E pour tout x, y > x0
On a donc f uniformément continue pour [x0,inf[
Et par théorème , f sur[0;x0] est uniformément continue car elle est continue sur un compact
Mais maintenant je bloque sur le cas ou x<x0<y vous pourriez me donner une piste ?
Merci
Soit f :R+->R et convergente et continue
f convergente , on apelle L sa limite , donc pour tout E >0 il existe x0>0 tq pour tout x >= x0 on a |f(x)- L|< E
On en déduit que |f(x)-f(y)|< E pour tout x, y > x0
On a donc f uniformément continue pour [x0,inf[
Et par théorème , f sur[0;x0] est uniformément continue car elle est continue sur un compact
Mais maintenant je bloque sur le cas ou x<x0<y vous pourriez me donner une piste ?
Merci
Re: Convergence uniforme pour une fonction convergente
Bonjour,
quelle est la question?
Je n'ai rien compris à ce que tu as écris, si ce n'est que tu t'es mal exprimé
quelle est la question?
Je n'ai rien compris à ce que tu as écris, si ce n'est que tu t'es mal exprimé
Re: Convergence uniforme pour une fonction convergente
Bonsoir , j'ai montré que f est uniformément continue pour tout x , y appartenant a [0;x0] , de meme pour [x0,inf[
mais maintenant il me manque plus que le cas ou x appartient a [0,x0] , et y appartient a [x0;inf[ ,j'aimerais bien avoir une piste sur comment résoudre ça
Merci
mais maintenant il me manque plus que le cas ou x appartient a [0,x0] , et y appartient a [x0;inf[ ,j'aimerais bien avoir une piste sur comment résoudre ça
Merci
Re: Convergence uniforme pour une fonction convergente
quelle est la définition de f continue?
quelle est la définition de f uniformément continue?
quelle est la définition de f uniformément continue?
Re: Convergence uniforme pour une fonction convergente
Ta démarche est bonne, mais avec des maladresses. Par exemple, n'écris pas "f est uniformément continue pour tout x , y appartenant à ...", ça n'a pas de sens. Aussi, si on sait que -L|<\epsilon) pour tout
pour tout 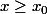 , on peut seulement en déduire que pour tous
, on peut seulement en déduire que pour tous 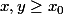 ,
, -f(y)|<2\epsilon) .
.
Essaie de reprendre les choses plus précisément. Tu te donnes un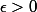 . Tu choisis un
. Tu choisis un  tel que pour tous
tel que pour tous 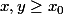 ,
, -f(y)|<\epsilon) (il faut pour cela modifier un peu ton argument). Ensuite tu peux utiliser la continuité uniforme de
(il faut pour cela modifier un peu ton argument). Ensuite tu peux utiliser la continuité uniforme de  sur
sur 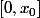 pour trouver un
pour trouver un  tel que ....
tel que ....
Reste effectivement à régler le cas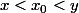 . Pour cela, tu peux utiliser la continuité de
. Pour cela, tu peux utiliser la continuité de  en
en  . Je te laisse voir.
. Je te laisse voir.
PS. Attention aussi, ne te mélange pas les pinceaux entre convergence uniforme et continuité uniforme (corrige ton titre).
Essaie de reprendre les choses plus précisément. Tu te donnes un
Reste effectivement à régler le cas
PS. Attention aussi, ne te mélange pas les pinceaux entre convergence uniforme et continuité uniforme (corrige ton titre).
Re: Continuité uniforme pour une fonction convergente
àMerci de ta réponse déja
Apres dire |f(x)-f(y)|<2E je pense que ça reste correct comme c'est pour tout E , si vraiment ça gène on prend |f(x)-L|<E/2 mais bon
Pour la continuité uniforme sur [0,x0] j'ai pas déterminer particulier "êta" particulier j'ai juste dis que par theoreme une fonction continue sur un compacte est uniformement continue .
Pour le cas ou je bloque j'ai pensé a dire que |x-x0|<|x-y|<eta mais est ce que cela implique que |f(x)-f(x0)|<|f(x)-f(y)|<E ??
Par exemple si on prend le cas d'une fonction croissante puis décroissante et on a x<x0<y on peut avoir que |f(x)-f(x0)|>|f(x)-f(y)| mais d'un autre coté on travaille sur des intervalles très petits donc je ne sais pas si ce que j'ai dit en haut est juste /
/
Apres dire |f(x)-f(y)|<2E je pense que ça reste correct comme c'est pour tout E , si vraiment ça gène on prend |f(x)-L|<E/2 mais bon
Pour la continuité uniforme sur [0,x0] j'ai pas déterminer particulier "êta" particulier j'ai juste dis que par theoreme une fonction continue sur un compacte est uniformement continue .
Pour le cas ou je bloque j'ai pensé a dire que |x-x0|<|x-y|<eta mais est ce que cela implique que |f(x)-f(x0)|<|f(x)-f(y)|<E ??
Par exemple si on prend le cas d'une fonction croissante puis décroissante et on a x<x0<y on peut avoir que |f(x)-f(x0)|>|f(x)-f(y)| mais d'un autre coté on travaille sur des intervalles très petits donc je ne sais pas si ce que j'ai dit en haut est juste
 /
/Re: Convergence uniforme pour une fonction convergente
Je finis par comprendre (ce n'était pas facile !) que tu veux montrer que si  est continue sur
est continue sur 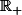 et a une limite finie en
et a une limite finie en  alors elle est uniformément continue.
alors elle est uniformément continue.
Tu disposes de deux relations :
... l'une au voisinage de l'infini où tu écris qu'il existe tel que
tel que -f(y)|<\varepsilon)
... l'autre où tu veux utiliser la continuité uniforme sur un compact.
L'astuce pour réussir la fin de la démonstration consiste à prendre un "intervalle de sécurité" où les deux relations sont vraies en même temps.
Par exemple, écrire la continuité uniforme sur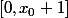 où tu disposes d'un certain
où tu disposes d'un certain  .
.
Pour finir tu prends) et tu considères
et tu considères  vérifiant
vérifiant 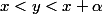 .
.
Puis tu considère les cas :
...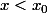 et du coup
et du coup 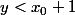 et tu peux majorer
et tu peux majorer -f(y)|) (grâce à la continuité uniforme sur
(grâce à la continuité uniforme sur 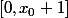
...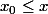 et tu peux AUSSI majorer la valeur absolue en utilisant la propriété de limite en
et tu peux AUSSI majorer la valeur absolue en utilisant la propriété de limite en 
Tu disposes de deux relations :
... l'une au voisinage de l'infini où tu écris qu'il existe
... l'autre où tu veux utiliser la continuité uniforme sur un compact.
L'astuce pour réussir la fin de la démonstration consiste à prendre un "intervalle de sécurité" où les deux relations sont vraies en même temps.
Par exemple, écrire la continuité uniforme sur
Pour finir tu prends
Puis tu considère les cas :
...
...
Re: Convergence uniforme pour une fonction convergente
Merci je pense avoir compris une partie ( l'intervalle de sécurité ) mais je ne comprends a quoi correspond "alpha" et pourquoi c'est le min de "eta" ; 1  /
/
La pour le coup j'ai essayé d'y reflechir mais je vois vraiment pas en quoi tout ça consiste
 /
/La pour le coup j'ai essayé d'y reflechir mais je vois vraiment pas en quoi tout ça consiste
Re: Convergence uniforme pour une fonction convergente
Kolis a écrit:Je finis par comprendre (ce n'était pas facile !) que tu veux montrer que siest continue sur
et a une limite finie en
alors elle est uniformément continue.
C'était ce que je voulais faire dire à l'intéressé, qui n'a jamais formulé entièrement la question
Re: Convergence uniforme pour une fonction convergente
Pour le choix de  c'est pourtant simple :
c'est pourtant simple :
Tu as un qui va bien sur le segment
qui va bien sur le segment 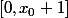
Mais il t'en faut un qui fasse mieux pour que l'écart entre assure de rester dans l'intervalle de chevauchement !
assure de rester dans l'intervalle de chevauchement !
Donc quelque chose plus petit que et aussi plus petit que
et aussi plus petit que  : ce
: ce  est anecdotique, tout réel strictement positif ferait l'affaire.
est anecdotique, tout réel strictement positif ferait l'affaire.
Tu as un
Mais il t'en faut un qui fasse mieux pour que l'écart entre
Donc quelque chose plus petit que
Re: Convergence uniforme pour une fonction convergente
Vous me dites si j ai bien compris parce que j en ai pas l air ..
L intervalle de chevauchement c est bien I= [x0;x0+1] ?
Donc on a bien pour x y appartenant à I : |x-y|<1
Mais si x n appartient pas à cette intervalle de chevauchement donc si x<x0 et y > x0 on peut prendre y bornée par x0 et x0+1 et là on peut dire que [0;x0] est un intervalle compact donc pour |x-y|<eta ==> |f(x)-f(y)|<E
Donc on réunie les 2 cas et on prend le min pour que ça soit toujours vrai si j ai bien saisi c est ça ?
L intervalle de chevauchement c est bien I= [x0;x0+1] ?
Donc on a bien pour x y appartenant à I : |x-y|<1
Mais si x n appartient pas à cette intervalle de chevauchement donc si x<x0 et y > x0 on peut prendre y bornée par x0 et x0+1 et là on peut dire que [0;x0] est un intervalle compact donc pour |x-y|<eta ==> |f(x)-f(y)|<E
Donc on réunie les 2 cas et on prend le min pour que ça soit toujours vrai si j ai bien saisi c est ça ?
Re: Continuité uniforme pour une fonction convergente
Ririyeman a écrit:àMerci de ta réponse déja
Apres dire |f(x)-f(y)|<2E je pense que ça reste correct comme c'est pour tout E , si vraiment ça gène on prend |f(x)-L|<E/2 mais bon
Pour la continuité uniforme sur [0,x0] j'ai pas déterminer particulier "êta" particulier j'ai juste dis que par theoreme une fonction continue sur un compacte est uniformement continue .
Pour le cas ou je bloque j'ai pensé a dire que |x-x0|<|x-y|<eta mais est ce que cela implique que |f(x)-f(x0)|<|f(x)-f(y)|<E ??
Par exemple si on prend le cas d'une fonction croissante puis décroissante et on a x<x0<y on peut avoir que |f(x)-f(x0)|>|f(x)-f(y)| mais d'un autre coté on travaille sur des intervalles très petits donc je ne sais pas si ce que j'ai dit en haut est juste/
Et est ce qu on peut me dire si cette méthode valable svp ?
Re: Convergence uniforme pour une fonction convergente
Ton message de 11:28 ne répond pas à la question de "continuité uniforme".
Tu ne peux pas jouer à borner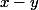 au gré de la position de
au gré de la position de  : il faut absolument trouver une borne intéressante pour
: il faut absolument trouver une borne intéressante pour 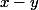 PUIS l'utiliser selon la position de
PUIS l'utiliser selon la position de  .
.
Tu ne peux pas jouer à borner
Re: Convergence uniforme pour une fonction convergente
D accord d accord et ducoup ce que j ai marqué juste au dessus c est bien ce que tu me dis , c est l idée ?
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
