Convergence uniforme locale

[rifly01]

Bonjour,


J'ai à étudier la convergence uniforme de la suite de fonctions de terme général :
[CENTER] [/CENTER]
1 - Sur R+
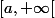
2 - Sur avec a>0

--- ce que j'ai fait :
1 - f_n converge simplement vers f, f la fonction nulle.
donc pas de convergnce uniforme sur

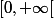
2 - Mon problème est ici.
Moi, j'aurai dit : tend vers 0 donc convergente uniformément vers 0 sur

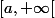
Ou bien,

Cette majoration est indépendente de , tend vers 0 donc il y a convergence uniforme vers 0 sur

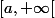
Et vous qu'auriez vous dit ?

Merci d'avance,

[klevia]

je pense que la convergence est unifprme sur [a, +oo[ d'ou CVU sur ]0,+oo[ mais pas sur [0,+ oo[

[rifly01]

Merci,
C'est ce que je pense aussi, Par contre comment tu aurais rédigé la question 2)

[kazeriahm]

je pense que la convergence est unifprme sur [a, +oo[ d'ou CVU sur ]0,+oo[ mais pas sur [0,+ oo[

non c'est faux

par exemple f_n(1/n)=n*exp(-1) ne tend pas vers 0 donc on a pas convergence sur ]0,l'infini[

c'est quand meme très différent de converger uniformément sur ]0,l'infini[ et sur [a,l'infini[ pour tout a puisque dans le premier cas on peut s'approcher de 0 aussi près qu'on veut (sans jamais l'atteindre bien sur), alors que dans le deuxieme cas bah on est bloqué

[klevia]

La rédaction me pose soucis... mais j'écrirais un truc du style:
Pour tous n, sup fn >= fn(1/n²)

or fn(1/n²) = 1 exp(-1/n) qui tend vers 1 quand n tends vers l'infini d'ou
sup fn >=1 d'où pas de convergence normale sur [0, +oo[

[klevia]

par exemple f_n(1/n)=n*exp(-1) ne tend pas vers 0 donc on a pas convergence sur ]0,l'infini[

J'étais d'accord avec toi, kazeriahm, mais ma prof, pas plus tard que Mercredi m'a dit que c'était automatique ... J'ai du mal comprendre la réponse ou elle mal comprendre la question ...

Merci de ta précison kazeriahm