[MP] Convergence uniforme et dérivation

[euler21]

Bonjour
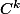
Si on se donne une suite de fonction telle que pour tout n, est de de classe . Si converge simplement vers une fonction f et si converge localement uniformément, est ce que cela est suffisant pour appliquer le théorème d'interversion de dérivée et de limites pour toutes les dérivées jusqu'à l'ordre k ??
Merci pour vos réponses

[Doraki]

J'vois pas comment tu peux appliquer le théorème ici.

[euler21]

Moi non plus :triste:
C'est une remarque que j'ai trouvé dans un cours de MP "assez célèbre" : elle dit qu'au lieu de supposer la convergence simple de toutes les dérivées jusqu'à l'ordre k-1, il suffit de montrer la convergence simple de

[Doraki]

Ben oui c'est un théorème un peu plus fort, mais pas super dur à montrer.

Si fn converge simplement et fn^(k) converge uniformément localement, alors pour 0<=i<=k tous les fn^(i) convergent simplement.

[euler21]

Une petite indication pour la démonstration s'il te plaît ??

[Doraki]

bah comme on avait commencé l'autre fois, on compare fn à la suite (gn = la k-ième primitive de fn^(k) dont toutes les dérivées d'ordre 0 jusqu'à k-1 s'annulent en 0).

[euler21]

Cela pour démontrer la convergence locale uniforme de .
Qu'en est il des dérivées ?? :mur:

[Doraki]

Je sais pas mais j'crois bien que toutes les suites (gn^(i)) convergent uniformément localement

[euler21]

euh comment ??

[Doraki]

Si une suite de fonctions continues (fn) converge localement uniformément vers f,
et si on définit la suite (Fn) où Fn = la primitive de fn qui vaut 0 en 0, et F = la primitive de f qui vaut 0 en 0,

Fn(x)-F(x) = intégrale de 0 à x de (fn(t)-f(t)) dt,
et en regardant bien, on peut montrer que Fn converge vers F localement uniformément.

Donc, dans le problème initial, la suite de fonctions pour laquelle on montre facilement que tout va pour le mieux au niveau dérivée/convergence, c'est bien la suite gn = la primitive k-ième de fn^(k) telle que gn(0)=gn'(0)=gn"(0)=...=gn^(k-1)(0) = 0. (on applique à (fn^(k)) k fois de suite le principe ci-dessus)

Ensuite il faut expliquer que la différence entre (fn) et (gn), on la connaît bien et en fait elle pose pas trop de problèmes :
Pour tout n il existe un polynôme Pn de degré (k-1) tel que fn(x) = gn(x) + Pn(x).
Pour tout x, Pn(x) = fn(x)-gn(x), donc Pn(x) a une limite P(x) quand n tend vers l'infini.

On peut montrer que cette fonction P est un polynôme et que chaque suite de coefficient de Pn converge vers le coefficient correspondant de P (une suite de polynômes de degré k, si ça converge, ça converge vachement bien)

Une fois qu'on a ce résultat très fort sur (Pn) = (fn-gn), y'a plus qu'à recoller les morceaux.

[euler21]

On peut montrer que cette fonction P est un polynôme et que chaque suite de coefficient de Pn converge vers le coefficient correspondant de P (une suite de polynômes de degré k, si ça converge, ça converge vachement bien)

Comment démontrer ce résultat s'il te plaît ?? (je pense pas qu'il est explicitement dans le cours MP)

[Doraki]

Si tu notes Pn (x) = somme des ai(n) x^i,
Eh ben tu peux obtenir les suites ai en fonction des suites Pn(0), Pn(1)... Pn(k-1)

La relation entre les (a0(n),...,a(k-1)(n)) et les (Pn(0),...,P(k-1)(n)) est linéaire, et la matrice est inversible (matrice de vandermonde).

Du coup chaque suite ai(n) s'écrit comme combinaison linéaire des suites Pn(0)...Pn(k-1), qui a donc une limite puisque Pn converge simplement.