Convergence d'une simple intégrale

[simplet]

Bonjour, je voudrais juste me fixer les idées avec la convergence de cette petite intégrale pour tout :


Moi je dis: soit un nombre A>1 alors < < .

Et < car la fonction est continue sur un borélien de mesure fini.
(J'ai le droit de dire ca?? Une fonction continue est intégrable sur un borélien de mesure finie? Ca ne m'a l'air pas horrible car si elle est continue sur cet intervalle elle y est bornée et donc l'intégrale est majorée par l'intégrale d'une constante sur un borélien de mesure finie)

mercii, en fait c'est ce dernier point le problème
mercii

[klevia]

Houla, ton niveau doit surement être supérieur au mien ... néanmoins , sauf erreur de ma part:
exp(-t) / t < exp(-t) quand t>1
Ainsi en intégrant entre x et N, on ontient donc

int ( exp(-t) / t) < int ( exp (-t))

or exp( - t ) est très facilement intégrale sur [x, N], tu fais ensuite tendre N vers l'infini et tu montres que ton integrale converge car plus petite ou égal qu'une intégrale qui converge !!!

Juste une remarque, j'ai oublié que toute tes intégrales étaient positives, c'est important !!

[klevia]

Pas de réponse !!! Dois-je en déduire que j'ai dit n'importe quoi ?

[BQss]

Bonjour, je voudrais juste me fixer les idées avec la convergence de cette petite intégrale pour tout :


Moi je dis: soit un nombre A>1 alors < < .

Et < car la fonction est continue sur un borélien de mesure fini.

Salut les gars,

En + l'infini c'est juste, tu peux aussi tout simplement remarquer que :


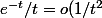pour la borne inferieur x, continue sur un borelien ne suffit pas, car cela ne garantie pas que ta fonction soit bornée, c'est continue sur un compact qu'il faut utiliser comme argument, ce qui fait que ta fonction est bornée sur [x;A] ou ]x;A[ peu importe : m<f(x)<M et donc l'integrale est compris entre et , etant fini et de valeure A-x, tu as ainsi egalement reglé le probleme pour la borne inferieur x et ton integrale converge.

[BQss]

[quote="klevia"]Houla, ton niveau doit surement être supérieur au mien ... néanmoins , sauf erreur de ma part:
exp(-t) / t 1
Ainsi en intégrant entre x et N, on ontient donc

int ( exp(-t) / t) 1, et ne reglera de toute facon ici que le probleme en l'infini car comme tu l'as dit ton inegalité n'est valable que pour t>1, il faut aussi traiter le probleme de la borne inferieur quand x<1 et on utilise un argument de continuité comme Simplet l'a fait.

[simplet]

Merci ,
je crois bien que c'est exactement le style de réponse que j'attendais: dans le même esprit que la mienne mais .. en plus juste!
mercii

[klevia]

Vous avez parfaitement raison, J'ai négligé ce problème pour x<1.
Il faut que j'apprenne à être plus rigoureuse ...
Merci de vos remarques constructives