Convergence d'une série

[tortue-geniale]

Salut,

J'arrive pas à démontrer que la série de terme général n/(n+1)! converge vers 1

Des pistes ?

[Matt_01]

Si on note la valeur recherchée est (après justification d'existence) f(1).
En dérivant cette série (après justification), on peut trouver la valeur de f'(x). Sachant que f(0)=0, on peut en déduire f(x) et donc f(1).

[tortue-geniale]

J'ai décroché à "Sachant que f(0)=0 on en déduit f(x)". Je vois pas pourquoi.

[Matt_01]

Si tu connais f', il suffit de connaître f en un point (ici 0) pour déterminer entièrement f.

[mathelot]

Salut,

J'arrive pas à démontrer que la série de terme général n/(n+1)! converge vers 1

Des pistes ?

On considère la fonction g définie par:


le problème posé revient à calculer g(1).

En ôtant des premiers termes et en dérivant, faire le lien entre g(x)
et l'exponentielle

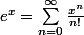
[Pythales]

On considère la fonction g définie par:


le problème posé revient à calculer g(1).

En ôtant des premiers termes et en dérivant, faire le lien entre g(x)
et l'exponentielle

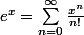
Autre méthode (variante) :

[zygomatique]

salut



série télescopique ....

:ptdr:

[Pythales]

salut



série télescopique ....

:ptdr:

Bien vu !!!