Convergence et sous-suites

[Dinozzo13]

Bonsoir, je fais un petit exercice sur les suites extraites et je tombe sur quelque chose de vrai alors que ça devrait être faux, merci de m'éclairer.

est définie sur et à valeurs dans .
Le but est de montrer (à l'aide d'un exemple) que bien que les suites et converge, il est possible que ne converge pas. Or moi je trouve que converge toujours !

Je ne demande pas qu'on me donne un exemple, j'aimerais en trouver un moi-même !
Je veux juste qu'on maiguille vers une piste :++:

[Doraki]

ben si tu comprends pourquoi ta preuve est fausse, tu trouveras un contre-exemple.

un carré ça peut valoir quoi modulo 3 ?

[Dinozzo13]

Ben justement non, je ne comprends pas pourquoi elle est fausse.

Ben un carré vaut 0 ou 1 modulo 3.
Je sens quelque chose mais je n'arrive pas à cerner pourquoi cette information est utile :cry:

[Skullkid]

Puisque qu'un carré vaut toujours 0 ou 1 modulo 3, les termes de sont parmi les termes de et . En exploitant cette information tu peux trouver ton contre-exemple.

[Dinozzo13]

Oui j'étais arrivé à cette conlcusion.
Peut-on dire que est une sous-suite de ou ?

En montrant que que ces trois dernières suites convergent toutes vers un même réel l, j'en déduis que c'est qui rend vrai l'affirmation.

[Dinozzo13]

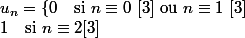
Il y a qui pourrait marcher, non ?

[Skullkid]

Oui, cette suite marche. Par contre il est faux de dire que est une sous-suite de (ou de ) puisque tous les carrés ne sont pas multiples de 3 (ou de la forme 3n+1)

[Dinozzo13]

Ok, peut-on dire que pour ou , est une sous-suite de et pour n\equiv 1 [3], (u_{n^2}) est une sous-suite de .

[Skullkid]

Non plus. Même si y a la lettre n dans le nom de la suite , elle ne dépend pas de n. C'est comme si tu disais un truc du genre "la fonction f est paire si x est positif".

[Doraki]

Pourquoi inventer des tournures de phrases alambiquées que personne va comprendre au lieu d'utiliser des notations normales.

Tu peux dire que (u(9n²)) est une sous-suite de (u(n²)) et de (u(3n)) ; tandis que (u((3n+1)²)) est une sous-suite de (u(n²)) et de (u(3n+1))

[Dinozzo13]

Pourquoi inventer des tournures de phrases alambiquées que personne va comprendre au lieu d'utiliser des notations normales.

Tu peux dire que (u(9n²)) est une sous-suite de (u(n²)) et de (u(3n)) ; tandis que (u((3n+1)²)) est une sous-suite de (u(n²)) et de (u(3n+1))

je suis trop bête alors
(je l'avais marqué au brouillon !)

[Dinozzo13]

oui, c'est comme ça que j'en ai conclus que et ont même limite.

Est-ce que et ont même limite ?

[Skullkid]

Si toutes les trois convergent, oui, c'est forcément vers la même limite. Tu as tous les éléments pour le démontrer si ça te chante.

[Dinozzo13]

Si toutes les trois convergent, oui, c'est forcément vers la même limite. Tu as tous les éléments pour le démontrer si ça te chante.

oui, je viens de le faire. ok, merci.

J'aimerai savoir par curiosité, si vous auriez trouvé de jolies suites qui vérifient la propriété énoncée.

[Skullkid]

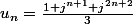
Ben celle que tu as trouvée est très bien... Qu'est-ce que tu entends par "jolie" ? Si c'est une formule directe en fonction de n que tu veux, on peut réécrire ta suite sous la forme avec j le nombre complexe habituel, mais c'est sans intérêt.

[Dinozzo13]

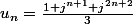
Ben celle que tu as trouvée est très bien... Qu'est-ce que tu entends par "jolie" ? Si c'est une formule directe en fonction de n que tu veux, on peut réécrire ta suite sous la forme avec j le nombre complexe habituel, mais c'est sans intérêt.

oui j'y avais pensé, mais est à valeurs réelles.

Oui, existe une formule en fonction de n.
ou alors une suite "élégante" pas nécessairement directement en fonction de n.

[Skullkid]

Mais est un réel quel que soit n. Ça vaut 0 quand n est congru à 0 ou 1 mod 3 et 1 sinon. Je t'ai dit : c'est la même suite que tu as donnée, mais réécrite de façon pédante.