Salut,
Si tu continue un peu à faire des maths., il faut ABSOLUMENT comprendre la différence entre ces deux trucs :
mehdi-128 a écrit:(1)
-f(x)| \leq \epsilon)
(2)
-f(x)| \leq \epsilon)
Dans le cas (1), vu où il est placé, le

a le droit de dépendre non seulement de

,
mais il a aussi le droit de dépendre de 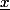
alors que dans le cas (2) ce même

ne droit de dépendre
que de 
et pas de

.
En fait, ça signifie que, dans le cas (1), la "vitesse" à laquelle fn(x) tend vers f(x)
peut dépendre de x (pour certains

, ça "tend rapidement", mais pour d'autres, ça va moins vite, voire pas vite du tout) alors que dans le (2), ça va "à la même vitesse pour tout les

.
L'idéal, comme toujours, c'est de voir ce que ça donne à l'aide d'un exemple : si on prend I=[0,1[ (ouvert en 1) et
\!=\!x^n)
, montre
uniquement avec la définition (
donc avec le (1)) que la suite de fonctions
_{n\geq 1})
converge
simplement vers la fonction nulle sur I=[0,1[.
Et donne même le "meilleur" (i.e. le plus petit)

possible.
Ensuite déduit en (toujours uniquement avec la définition, c'est à dire avec le (2) et sans utiliser un quelconque théorème) qu'il n'y a pas convergence uniforme de
_{n\geq 1})
sur I=[0,1[.
mehdi-128 a écrit:(2)
-f(x)| \leq \epsilon})
Sinon, concernant ta deuxième question, vérifie que la partie en bleue çi dessus dit exactement la même chose que
\!-\!f(x)|\big)\leq\!\varepsilon)
puis que le début de la phrase (resté en noir) dit précisément que ce sup (qui dépend de n) tend vers 0 lorsque n tend vers l'infini.
