Convergence simple jamais uniforme

[Nightmare]

Re bonjour :happy3:

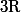
Toujours dans mes séries de fonctions, je me suis mis à chercher une suite de fonctions continues convergeant simplement vers 0 sur mais ne convergeant uniformément sur aucun compact.

J'en ai a priori trouvé une, et vous, vous en avez une en tête?

:happy3:

[Doraki]

Tu veux dire une suite de fonctions ?

fn(x) = 1 si x est rationnel et son dénominateur vaut n, 0 sinon ?

[Nightmare]

Salut Doraki :happy3:

Mes excuses j'ai oublié un mot important dans mon énoncé : suite de fonctions continues !

[Doraki]

Dans ce cas je prends une suite de fonctions affines par morceaux

Pour p>n>0, f(n,p)(x) = un pic de hauteur 1/n et de largeur 1/p posé à droite des rationnels de dénominateur n. (si x est un tel rationnel, f(n,p)(x)=0, f(n,p)(x+1/2p) = 1/n, f(n,p)(x+1/p) = 0)

Pour tout x et epsilon, il n'y a qu'un nombre fini de (n,p) tels que f(n,p)(x) > epsilon. Donc la suite converge simplement vers 0.

Pour tout ouvert il y a un rationnel dans son intérieur, donc il existe un epsilon tel qu'il y a une infinité de fonctions qui passent au-dessus de epsilon sur cet ouvert.
Donc la convergence n'est uniforme sur aucun compact.