[L2] Convergence de séries et décomposition

[ThPra]

Hello!

Je révise pour mes examens et j'ai quelques interrogations sur certains exo que j'ai trouvé dans des anciens sujets, les voici:



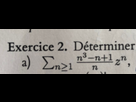
On me demande de calculer la somme de la série. Généralement pour se faire on fait d'abord une décomposition en plusieurs fractions et on joue avec les coefficients et les développements limités, sauf que là je ne vois pas comment faire la décomposition.
On a déjà eu ce genre de série à décomposer mais je n'avais pas non plus compris la décomposition du prof:

"On écrit par division euclidienne puis décomposition en éléments simples :
n²/(n-1)(n-2) = 1 - 1/(n-1) + 4/(n-2) "

Sinon j'ai aussi un problème pour calculer le rayon de convergence des séries de la forme suivante: Σ(1+(-1)^n²)z^n

Généralement pour faire sauter les (-1)^n on utilise le quotient avec les valeurs absolues, sauf qu'ici on est dans une somme donc ça ne permet pas de s'en débarrasser (j'ai aussi eu une série de la forme 1+(-2)^n et je suis encore plus perdu)

Merci d'avance!

[phyelec]

Bonjour,

pour
on a :

donc






a+b=3 et 2a+b=2 soit a=-1 et b=4

[ThPra]

Merci beaucoup je n'avais jamais pensé à ce genre de technique!

Mais du coup comment faire pour la série de l'image étant donné qu'aucune factorisation n'est possible ?
J'ai tout essayé pour transformer l'expression mais ça ne mène à rien

[Ben314]

Salut,
Concernant les décompositions en éléments simple, là, ça va qu'il n'y a que 2 pôles (donc un système de deux équations à deux inconnues à résoudre), mais dans le cas de pôles simples (i.e. le dénominateur n'a que des racines simples), c'est quand même bien plus rapide d'écrire que, vu les degrés du numérateur et du dénominateur, la théorie te vend qu'on a :

puis,
a) En faisant tendre on obtient .
b) En multipliant à droite et à gauche par puis en prenant on a .
c) En multipliant à droite et à gauche par puis en prenant on a .

Et concernant , ben y'a besoin de zéro théorie pour immédiatement voir que c'est égal à .

[tournesol]

Bonjour à tous
sum nz^n=z sum nz^(n-1)
sum nz(n-1) se calcule par primitivation puis dérivation

[ThPra]

Salut,
Concernant les décompositions en éléments simple, là, ça va qu'il n'y a que 2 pôles (donc un système de deux équations à deux inconnues à résoudre), mais dans le cas de pôles simples (i.e. le dénominateur n'a que des racines simples), c'est quand même bien plus rapide d'écrire que, vu les degrés du numérateur et du dénominateur, la théorie te vend qu'on a :

puis,
a) En faisant tendre on obtient .
b) En multipliant à droite et à gauche par puis en prenant on a .
c) En multipliant à droite et à gauche par puis en prenant on a .

Et concernant , ben y'a besoin de zéro théorie pour immédiatement voir que c'est égal à .

Merci pour votre réponse.

Mais comment faites vous le lien entre les coefficients de la fraction et la formule qu'on va avoir ? J'ai regardé beaucoup de vidéos mais à chaque fois c'est le cas où le numérateur a un plus petit degré que le dénominateur, jamais l'inverse comme j'ai ici...

Pour la deuxième fraction je suis d'accord qu'on peut diviser chaque terme par n (attention c'est bien n^3 et pas n^2) mais une fois que j'ai n^2-1+1/n, je sais que 1/n * z^n vaut -ln(1-z), mais que puis-je faire avec n^2-1 ? je pourrais le factoriser avec l'identité remarquable mais ça mène à rien...

merci d'avance

[Ben314]

Mais comment faites vous le lien entre les coefficients de la fraction et la formule qu'on va avoir ? J'ai regardé beaucoup de vidéos mais à chaque fois c'est le cas où le numérateur a un plus petit degré que le dénominateur, jamais l'inverse comme j'ai ici...

Ben ça, c'est un truc qu'on comprend normalement bien avant de faire des réductions en éléments simples, à savoir la notion de division euclidienne (de polynômes) : lorsque l'on divise un polynôme de degré par un polynôme de degré , on a avec de degré donc et pour que soit de degré il faut que soit de degré donc que soit de degré .

...mais une fois que j'ai n^2-1+1/n, je sais que 1/n * z^n vaut -ln(1-z), mais que puis-je faire avec n^2-1 ? je pourrais le factoriser avec l'identité remarquable mais ça mène à rien...

Tu scinde simplement en 2 : le d'un coté et le de l'autre.
- Pour le , ça te donne dont la valeur est connue depuis le Lycée.
- Pour le ça te donne et là, tu utilise ce que t'a dit tournesol, à savoir que pour "faire apparaître" du , il suffit de dériver : si alors (dans le disque de convergence).
Et si tu veut du et pas du , ben c'est con comme la lune : il suffit de multiplier par :

[tournesol]

donc

[ThPra]

Merci pour vos réponses!

Alors je comprends les calculs que Ben fait pour n² (on a un exo-type où il faut résoudre des équations différentielles et faire des calculs sur les sommes) par contre je ne comprends pas ce qu'il faut en tirer...
J'imagine que le but est de se rapprocher d'une somme connue/d'un développement limité mais je ne vois pas le rapport entre n²z^n et ncnz^n.

Je comprends aussi les calculs de tournesol mais jamais je ne pourrai penser à ces raisonnements le jour de l'exam (par exemple la façon de décomposer n^2 me semble pas du tout naturel même si la suite semble accessible)