Convergence de série

[pierlucke]

Bonjour à tous, j'ai un probleme de convergence de série à résoudre...
c'est a dire que je dois démontrer si la série converge ou non.
la série est ln2/2 + ln3/3 +ln4/4 + ln5/5 ce que j'ai trouvé a présent est que le terme general de cette série est Ln (n+1)/n+1.....et que ce terme tend vers 0 si on vérifie sa limite quand n tend vers l'infini. Cependant, cette condition est essentielle , mais non concluente pour démontrer que la série converge ou pas....J'ai de disponible pour prouver cela:
1-le test d'Alembert,
2-test de comparaison (que je trouve tres difficile a utiliser car je ne connais pas beaucoup de séries
3-le test de l'intégrale de Cauchy (qui ici ne s'applique pas je crois car la série n'est pas entièrement décroissante (elle l'est seulement a partir de n=e-1), mais je crois que je pourrais l'utiliser car so on retranche n=1 de la série cela n'a pas d'impact sur sa convergence ou divergence...Vrai?
4)Test polynome (ici =non applicable)
5) test racine n eme de Cauchy

Je ne sais pas par quoi commencer , je vais continuer a chercher de mon coté, mais si quelqu'un pourrait m'aider , j'aimerais bien...

Merci a tous

[_-Gaara-_]

Bonsoir,

a mon avis Un = ln(n)/n est positive, décroissante et de limite nulle (à vérifier pour la décroissance par tes soins) donc la somme Sigma (-1)^n Un converge ensuite essaye de voir avec des majorations du style Sigma S_2n+1< Sigma (-1)^n Un < S_2n

[pierlucke]

Salut, merci pour la réponse, je ne comprend cependant pas la section sur les sigma , Est ce que c'est des sommations?...Quelqu'un peut me donner des details avec Les Vérificateurs de convergence plus haut?

[pierlucke]

J'ai retravaillé un bon 2 heures sur mon probleme et je crois que je doit comparer la série
Ln (n+1)/n+1 avec un série divergente connu ou tous les termes sont inférieurs a la série du probleme.....pour prouver la divergence de la première

Ou la comparer avec une autre série qui est supérieur qui converge pour affirmer sa convergence....

Il faut noter que ce sont des séries et non des suites...

Merci de m'aider :cry:

[_-Gaara-_]

Salut,
bon désolé je n'ai pas très bien rédigé mais oublie mon idée lol ;)

j'ai trouvé un peu mieux,
ça s'appelle "séries de bertrand" :D

tu as que la série de terme géneral Un=1/n^a * 1/(ln(n))^b converge si et seulement si a>1 ou (a=1 et b>1)

ici tu as a<=1 et b=<1 donc c'est bon IMHO :we:

la démo est assez simple si ça t'intéresse :D

[skilveg]

Gaara, on a souvent , et est le terme général d'une série notoirement divergente, non?

[_-Gaara-_]

oui pour n>= 2 ^^ je n'y avais pas pensé sorry :D mais ma méthode marche !! x)
et puis maintenant on a 2 solutions, ce qui vaut toujours mieux qu'une seule :++:

[skilveg]

Oui! ^^ Mais c'est l'éternelle différence entre le marteau-pilon et la pichenette ;)

[_-Gaara-_]

j'aime bien cette analogie XD ^^

[pierlucke]

Merci, ca marche maintenant! J'ai utilisé la méthode qui compare avec 1/n...simple et efficace

A+

[PhiD]

Bonjour,

Je suis nouveau sur le forum et je sens que je vais être un très grand abonné tellement les informations trouvées sur le site sont excellentes. Je vous remercie d'ores et déjà pour votre soutien et le travail déjà accompli.

Je suis navré de présenter le travail sans aucune contribution, et dans un état brut. Je sais que reprendre les études va être dur, et je désire progresser le plus possible.

Voici l'énoncé que j'ai du mal à comprendre, je reprends les études après un long moment d'arrêt ;

Soit (Un) n>= 1 une suite de nombre réels. On suppose Un > 0 pour tout n>=1 et qu'il existe a élément de R et c élément de R tels que :

Un+1/Un = 1 - a/n + c/n^2 +O(1/n^2)

a) Montrer que la série Somme de Un (infini) converge si a > 1 et diverge si a < 1.

b) Si a=1. Par comparaison avec une série de terme général 1/(n+d), avec d élément de R bien choisi. étudier la convergence de la série Somme Un (infini) de terme général.

En utilisant le résultat de la question précédente et étant donné alpha élément de R/N, étudier, en discutant selon la valeur de alpha, la convergence de la série Somme Un de terme général :

Un = (|alpha|x |1 - alpha|x|2-alpha|x (...) x |n - 1 - alpha|) / n! = (PI(k=0, n-1) |k - alpha| ) / n!

Je vous remercie vivement.

Cordialement,

[Ben314]

Salut,
a) Si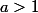 on peut choisir un puis, grâce à l'hypothèse, montrer qu'il existe un N tel que, pour , on ait ) c'est à dire que ce qui prouve que la série 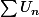est convergente.

Même méthode (quasiment...) pour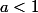 où on prend et ou on montre que est minorée par une série positive divergente donc est elle même divergente.

b) Si on veut montrer... quoi que ce soit, il faut évidement supposer que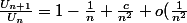 avec un "petit o" et pas un "grand O" (car sinon le ne sert absolument à rien...). On procède de même en encadrant en utilisant deux constantes et telles que ...

[Vupen]

On déduit façilement que )

Je me doute qu'il y a du télescopage dans l'air mais je ne vois pas d'où sort le ln(n) en fait

Merci

[Ben314]

Le il sort de la somme des -b/k avec k entre N et n (comparaison somme/intégrale)

[PhiD]

Salut,
a) Si on peut choisir un puis, grâce à l'hypothèse, montrer qu'il existe un N tel que, pour , on ait ) c'est à dire que ce qui prouve que la série est convergente.

Même méthode (quasiment...) pour où on prend et ou on montre que est minorée par une série positive divergente donc est elle même divergente.

b) Si on veut montrer... quoi que ce soit, il faut évidement supposer que avec un "petit o" et pas un "grand O" (car sinon le ne sert absolument à rien...). On procède de même en encadrant en utilisant deux constantes et telles que ...

Merci beaucoup