Convergence série numérique

[Maria201]

Bonjour,
je dois étudier la nature (convergente/divergente) de la série de terme général

<a href='https://www.casimages.com/i/200531020524841910.png.html' target='_blank' title='Mon image'><img src='https://nsa40.casimages.com/img/2020/05/31/200531020524841910.png' border='0' alt='Mon image' /></a>

mais Cauchy ne donne rien, d'Alembert une limite indéterminée, et je ne suis pas arrivé à trouver un équivalent... pouvez - vous m'aider ??

merci !

[Mateo_13]

Bonjour,



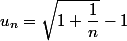
J'avais mal lu l'énoncé, je croyais qu'il s'agissait de la suite, pas de la série. Désolé.

Cordialement,
--
Mateo.

[Rdvn]

Bonjour
D'abord montrer (c'est très facile) qu'il s'agit d'une série à termes positifs :
on peut alors utiliser le critère d'équivalence .
On peut trouver un équivalent simple en utilisant un développement limité pour la racine carrée, ou bien en multipliant et divisant par la quantité conjuguée
(c'est rc(1+(1/n))+1)
Bon courage
Revenez au besoin, avec un premier essai

[Maria201]

Bonjour
D'abord montrer (c'est très facile) qu'il s'agit d'une série à termes positifs :
on peut alors utiliser le critère d'équivalence .
On peut trouver un équivalent simple en utilisant un développement limité pour la racine carrée, ou bien en multipliant et divisant par la quantité conjuguée
(c'est rc(1+(1/n))+1)
Bon courage
Revenez au besoin, avec un premier essai

Merci pour votre réponse !!!
J'ai trouvé que 1/2n était un équivalent
C'est bien ça ??
Et du coup on peut comparer ma série à la série harmonique qui diverge ?

[Rdvn]

C'est bien cela, il suffit d'ailleurs de présenter l’équivalent sous forme
(1/2).(1/n) et c'est du cours : série divergente
Bonne journée