Convergence de série (licence 2)

[Vindic]

Bonjour,

Alors voilà, j'ai un problème avec les convergences d'intégrales de séries de fonctions. Ma première question serait une clarification:
est-elle une condition suffisante pour dire qu'une série de fonctions converge ?
est-elle une condition suffisante pour dire que converge ?

Deuxième partie, l'exercice que je n'arrive pas à faire !
Soit
Montrer que converge simplement sur R.
Pour a >0 montrer que converge normalement sur


Merci beaucoup !

[Sylviel]

\lim_{x \to \infty} f_n(x) = 0 est-elle une condition suffisante pour dire qu'une série de fonctions f_n converge ?

Pour tout n j'imgines ? Quoi qu'il en soit non, cela signifie que la limite en plus l'infini est nulle, pas que la suite de fonctions a une propriété quelconque.

\lim_{x \to \infty}f(x) = 0 est-elle une condition suffisante pour dire que \int_0^\infty f(x)dx converge ?

1/x

Il manque trop de choses dans ta deuxième partie pour en tirer quoi que ce soit : que vaut f ? L'intégrale est prise sur quoi ? etc...

[Vindic]

Il manque trop de choses dans ta deuxième partie pour en tirer quoi que ce soit : que vaut f ? L'intégrale est prise sur quoi ? etc...

Autant pour moi ! J'ai corrigé les erreurs.

[girdav]

Pour la deuxième partie penser aux séries de la forme .

[math_nour]

Bonjour,


est-elle une condition suffisante pour dire qu'une série de fonctions converge ?

c'est une condition nécessaire et non suffisante

Deuxième partie, l'exercice que je n'arrive pas à faire !
Soit
Montrer que converge simplement sur R.

essaye de majorer

Pour a >0 montrer que converge normalement sur
Merci beaucoup !

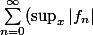calcule le sup de car une série converge normalement si et seulement si converge