Convergence série de fonctions

[iamsebfont]

Bonjour,

je n'arrive pas à prouver que


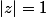
dont le rayon de convergence est r=1, est convergente pour tout z appartenant au complexe tq et

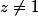
En français : Montrez que la fonction converge sur le bord du disque de rayon 1 sauf en z=1..

Merci pour l'aide

[yos]

Connais-tu la règle de D'Abel sur les séries semi-convergentes?

[iamsebfont]

Non, je ne la connais pas (en tout cas, pas sous ce nom là .. mais donne la toujours)

[yos]

La règle d'Abel :
Si est une suite réelle décroissante, convergeant vers 0 et une suite de complexes telle que soit majoré indépendamment de n et de m, alors la série 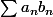converge.
Tu peux observer que :

• ce théorème généralise le théorème sur les séries alternées;
• il n'y a pas lieu de l'utiliser si la série 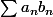est absolument convergente.

Ici ça te permet de conclure en posant et pour .

Alors que le théorème des séries alternées ne marche que pour z=-1.

Mais si tu l'as pas vu, faudrait peut-être envisager autre chose : comparaison avec une intégrale.

[iamsebfont]

Si je l'ai vu, on l'a juste appelé le test de DEDEKIND.

Merci !

[yos]

on l'a juste appelé le test de DEDEKIND.

Ca alors! Après le mépris que lui a accordé Cauchy, voilà Abel pillé par Dedekind. Ton professeur ne serait-il pas pro-germanique?