Convergence normale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 15:22
-
 par zork » 30 Déc 2011, 21:06
par zork » 30 Déc 2011, 21:06
bonsoir
j'aurai une besoin d'un coup de pouce sur cette série: x dans R
} {n!} x^(^2^n^))
j'ai trouvé qu'elle valait 1
dans la suite on me demande de montrer que la série converge normalement sur tout intervalle [a,b] quels que soient les réels a<b
j'ai majoré le terme général de la série par x^(2n) mais le problème c'est que la série x^(2n) ne converge pas toujours puisque x est dans R
comment faire?
dans la seconde question on me demande d'étudier la convergence uniforme sur R
Déjà avec ce qui précéde elle converge uniformément sur [a,b]
mais comment montrer qu'elle ne converge pas uniformément sur R?
merci pour votre aide

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 30 Déc 2011, 22:17
par raito123 » 30 Déc 2011, 22:17
Tu as trouver que la série vaut 1 ?
Les multiples ne doivent pas être utilisés sans nécessité
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 15:22
-
 par zork » 31 Déc 2011, 12:28
par zork » 31 Déc 2011, 12:28
oui j'ai trouvé qu'elle valait 1
-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 31 Déc 2011, 12:47
par Le_chat » 31 Déc 2011, 12:47
Si tu évalues en 1, ça fait e^2, donc ça m'étonnerait que cette série fasse 1.
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 15:22
-
 par zork » 31 Déc 2011, 13:02
par zork » 31 Déc 2011, 13:02
je suis vraiment c**
dans la série ce n'est pas exp(x²) mais exp(-x²)
-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 31 Déc 2011, 14:08
par Le_chat » 31 Déc 2011, 14:08
Ca ne change pas le problème, ça fait 0 en 0.
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 15:22
-
 par zork » 31 Déc 2011, 14:23
par zork » 31 Déc 2011, 14:23
j'ai fais comme ceci:
exp(x)=
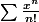
donc
} {n!})
=exp(x²)
en multipliant par exp(-x²) j'obtiens 1
ou je fais une erreur?

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 31 Déc 2011, 14:40
par raito123 » 31 Déc 2011, 14:40
on parle de
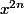
ou bien de
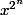
dans la série ?
Les multiples ne doivent pas être utilisés sans nécessité
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 15:22
-
 par zork » 31 Déc 2011, 16:38
par zork » 31 Déc 2011, 16:38
on parle de
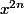
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 15:22
-
 par zork » 01 Jan 2012, 15:18
par zork » 01 Jan 2012, 15:18
je me permet de relancer le post
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 01 Jan 2012, 15:42
par girdav » 01 Jan 2012, 15:42
Est-ce que tu peux récapituler les modifications en éditant le post initial ?
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 15:22
-
 par zork » 01 Jan 2012, 16:20
par zork » 01 Jan 2012, 16:20
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 01 Jan 2012, 16:35
par girdav » 01 Jan 2012, 16:35
Pour la convergence normale sur tout intervalle borné, par quoi peux tu majorer

si

? Et si

?
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 15:22
-
 par zork » 01 Jan 2012, 17:03
par zork » 01 Jan 2012, 17:03
j'aurai majoré le terme général de la série de départ par x^(2n)
comme x dans [a,b]
x^(2n)<=b^(2n)
mais il faudrait des renseignements sur b?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 01 Jan 2012, 21:20
par girdav » 01 Jan 2012, 21:20

, qui est le terme général d'une série convergente.
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 15:22
-
 par zork » 03 Jan 2012, 15:06
par zork » 03 Jan 2012, 15:06
dans la seconde question on me demande la convergence uniforme de la série sur R
déjà comme il y a convergence normale sur tout segment [a,b] elle converge uniformément sur [a,b]
mais comment montrer qu'il n'y a pas convergence uniforme sur R?
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 03 Jan 2012, 16:24
par Maxmau » 03 Jan 2012, 16:24
zork a écrit:dans la seconde question on me demande la convergence uniforme de la série sur R
déjà comme il y a convergence normale sur tout segment [a,b] elle converge uniformément sur [a,b]
mais comment montrer qu'il n'y a pas convergence uniforme sur R?
Bj
peut-être faire appel à un théorème de permutation de limites utilisant la CU ?
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 15:22
-
 par zork » 03 Jan 2012, 16:35
par zork » 03 Jan 2012, 16:35
ce théorème: un(x) continue
si
)
converge uniformément alors on peut intervertir série et intégrale?
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 03 Jan 2012, 16:54
par Maxmau » 03 Jan 2012, 16:54
zork a écrit:ce théorème: un(x) continue
si
)
converge uniformément alors on peut intervertir série et intégrale?
ou série et limite en x=infini
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 15:22
-
 par zork » 03 Jan 2012, 16:59
par zork » 03 Jan 2012, 16:59
il y a quelque chose que je comprend pas:
comment montrer que série et limite ne peuvent pas être interverti?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
