Convergence normale série de suites

[rocket22]

bonsoir !

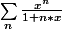
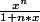
comment peut-on montrer (ou non) la convergence normale de la série sur l'intervalle [0,1[ ? Si on pose f_n(x) = et qu'on étudie les variations, on voit que f'_n s'annule en 1 et est positive sur l'intervalle d'étude mais ça ne nous donne pas de sup...

et je ne vois pas de majoration de ||f_n|| (borne sup sur [0, 1[)

[mathelot]

Bonsoir,
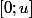
la convergence est normale sur tout intervalle compact avec

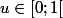
[rocket22]

alors comment montrer que la série n'est pas normalement convergente sur [0,1[ qui n'est pas un compact?

[tournesol]

Ça te donne le sup puisque ta fonction fn est continue et strictement croissante sur [0;1]
Ton sup , c'est fn(1)=1/(1+n) et comme c'est le terme général d'une série divergente...