Convergence faible d'une suite et opérateur compact

[melreg]

Bonjour,

Voici mon problème:
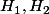
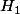
Soient deux espaces de Hilbert et un opérateur compact. Si une suite de converge faiblement vers x (i.e ), alors est-ce que l'on a ?

Si oui, pourquoi?
Merci d'avance

[melreg]

Je comprends que le titre vous fasse peur, mais je crois qu'il n'y a pas de quoi, pour quelqu'un d'habitué...
A l'aide !!!

[L.A.]

Bonjour,

Le problème est que tu ne donnes pas assez de définitions, il n'y a que toi qui sait de quoi tu parles alors personne ne peut t'aider.

Moi je crois savoir qu'un espace de Hilbert a rapport avec la completude, mais par contre j'ai jamais entendu parler d'opérateur compact.

si je peux aider ce serait avec plaisir, bien que je pense que mon niveau est inferieur au tien.

[Doraki]

Soit w dans H2.
T est compacte donc continue, et donc l'application x -> est une forme linéaire continue de H1.
Donc tu peux appliquer le théorème de représentation de Riesz.

[melreg]

Tu as sûrement raison Doraki. Voici quelques précisions :

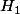
Un opérateur linéaire ( sont des espaces de Hilbert) est dit compact si l'image de toute partie bornée de par T est relativement compacte (i.e. d'adhérance compacte) dans .
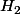
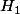
OU de manière équivalente, si de toute suite bornée dans , on peut extraire une sous-suite telle que converge dans .

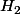
Je pense que la seconde défintion est plus maniable (en tout cas ici...).

Est-ce que c'est plus clair pour vous?