Bonjour,
Je n'arrive plus a montrer ce théorème qui ressemble a celui de la convergence dominnée de Lebesgue:
Si f_n est une suite fonctions integrables convergent presque surement vers f (aussi integrable), si la norme L1 de f_n converge vers la norme L1 de f (ie, l'integrale |f_n| cv. vers |f|), alors f_n converge vers f en norme L1.
Ca doit etre assez simple...mais je ne vois pas comment utiliser la seconde hypothese.
Convergence dominée
6 messages
- Page 1 sur 1
par ThSQ » 09 Nov 2008, 10:01
Quelques idées, sans garantie :
Déjà j'ai l'impression qu'on peut se ramener à
quitte à remplacer f_n par |f_n|
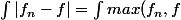 \, - \, \int min(f_n, f))
 = \int f_n \,+ \,\int f \,- \,\int min(f_n,f))
Donc ça revient à montrer que \rightarrow \int f)
Méeh \leq f)
il y a de la convergence dominée pas loin.
Déjà j'ai l'impression qu'on peut se ramener à
Donc ça revient à montrer que
Méeh
par balba » 09 Nov 2008, 10:54
Merci. Je pense que ca marchera pas comme ca cependant...
En effet ce que tu peux montrer, ce sera que |f_n| tend vers |f| en norme L1, mais pas f_n vers f.
En effet ce que tu peux montrer, ce sera que |f_n| tend vers |f| en norme L1, mais pas f_n vers f.
par ThSQ » 09 Nov 2008, 11:27
Tu as raison, mais il est peut-être possible de se passer de l'hypothèse f_n > 0
par ThSQ » 09 Nov 2008, 16:14
Je sais pas si c'est encore utile mais je crois que je l'ai :
 | \leq | f_k(x) - f(x) | + | f(x) |)
donc
 - f(x) | - | f_k(x) | + | f (x)|)
et  - f(x) | - | f_k(x) | + | f(x) | \leq .... \leq 2 | f |)
On peut appliquer la conv dominée à - f(x) | - | f_k(x) | + | f (x)| \rightarrow 0)
c'est à dire
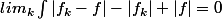
mais
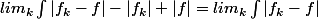
vu les hypothèses, finito
donc
On peut appliquer la conv dominée à
c'est à dire
mais
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :