Contraposée d'une application
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
superkader5
- Membre Relatif
- Messages: 103
- Enregistré le: 17 Déc 2007, 20:09
-
 par superkader5 » 10 Mar 2008, 22:57
par superkader5 » 10 Mar 2008, 22:57
bonjour! je voudrais savoir quel est la contraposée de:
(lorsque (pn) converge on note p sa limite)
sum(Un²) converge --->(pn) converge et p est non nul
donc moi j'hésite entre
1) (pn) ne converge pas vers p ou p est nul---> sum(Un²) diverge
ou
2) (pn) diverge ---> sum(Un²) diverge
A mon avis la plus logique serait la premiere mais le probleme dans ce cas ci c'est que je doit supposé un des deux cad ((pn) ne converge pas vers p
ou p non nul) ou je doit supposé les 2 en meme tps enfin c'est un peu dur a comprendre!
jespere que vous avez compris merci a bientot!
-
trust
- Membre Relatif
- Messages: 163
- Enregistré le: 30 Oct 2007, 20:01
-
 par trust » 10 Mar 2008, 23:00
par trust » 10 Mar 2008, 23:00
je dirais la première
-
superkader5
- Membre Relatif
- Messages: 103
- Enregistré le: 17 Déc 2007, 20:09
-
 par superkader5 » 10 Mar 2008, 23:03
par superkader5 » 10 Mar 2008, 23:03
oué mais jtrouve que c'est assez bizarre parce que si p est la limite de (pn) alors si (pn) ne converge pas vers p ben forcément (pn) diverge non?
-
trust
- Membre Relatif
- Messages: 163
- Enregistré le: 30 Oct 2007, 20:01
-
 par trust » 10 Mar 2008, 23:06
par trust » 10 Mar 2008, 23:06
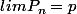
?
 par alavacommejetepousse » 10 Mar 2008, 23:08
par alavacommejetepousse » 10 Mar 2008, 23:08
bonsoir
je n'ai pas compris l'implication
Un ; pn
peux tu réécrire avec des quantificateurs
-
superkader5
- Membre Relatif
- Messages: 103
- Enregistré le: 17 Déc 2007, 20:09
-
 par superkader5 » 10 Mar 2008, 23:10
par superkader5 » 10 Mar 2008, 23:10
oui (pn) c'est une suite mais je suis pas d'accord avec ce que vous dites parce qu'il me semble qu'une suite soit elle converge soit elle diverge donc apres la je suis encore + dans le flou
-
superkader5
- Membre Relatif
- Messages: 103
- Enregistré le: 17 Déc 2007, 20:09
-
 par superkader5 » 10 Mar 2008, 23:15
par superkader5 » 10 Mar 2008, 23:15
dsl mais je narive pas a écrire avec les quantificateurs ici mais ce qui est important c'est que lorsque la suite (pn) converge alors on note p sa limite et lorsqu'elle diverge on note +infinie ou -infinie sa limite.
apres mon implication est:
somme(un²) converge implique (pn) converge et p non nul
-
trust
- Membre Relatif
- Messages: 163
- Enregistré le: 30 Oct 2007, 20:01
-
 par trust » 10 Mar 2008, 23:22
par trust » 10 Mar 2008, 23:22
la suite
)_{n})
converge? diverge?
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 10 Mar 2008, 23:23
par abcd22 » 10 Mar 2008, 23:23
Bonsoir,
Le contraire de « (p_n) converge et sa limite p est non nulle », c'est « (p_n) diverge ou converge vers 0 ».
Une suite divergente ne tend pas forcément vers + ou - l'infini, (-1)^n n'a pas de limite par exemple.
-
trust
- Membre Relatif
- Messages: 163
- Enregistré le: 30 Oct 2007, 20:01
-
 par trust » 10 Mar 2008, 23:25
par trust » 10 Mar 2008, 23:25
je dirais " ne converge pas ou tend vers 0 "
-
superkader5
- Membre Relatif
- Messages: 103
- Enregistré le: 17 Déc 2007, 20:09
-
 par superkader5 » 10 Mar 2008, 23:27
par superkader5 » 10 Mar 2008, 23:27
ah okok merci abcd22 mais en suposant que pn diverge ou p=0
est ce que je doit suposé les 2 en meme temps ou suposé un des deux?????????
-
superkader5
- Membre Relatif
- Messages: 103
- Enregistré le: 17 Déc 2007, 20:09
-
 par superkader5 » 10 Mar 2008, 23:29
par superkader5 » 10 Mar 2008, 23:29
ben oui (sin n)n diverge car une suite qui n'a pas de limite une suite qui n'a pas de limite est considéré comme divergente
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 10 Mar 2008, 23:43
par abcd22 » 10 Mar 2008, 23:43
trust a écrit:je dirais " ne converge pas ou tend vers 0 "
« ne converge pas », c'est synonyme de « diverge ».
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 10 Mar 2008, 23:44
par abcd22 » 10 Mar 2008, 23:44
superkader5 a écrit:est ce que je doit suposé les 2 en meme temps ou suposé un des deux?????????
« ou » ça veut dire qu'on suppose un des deux, sinon c'est « et ».
-
superkader5
- Membre Relatif
- Messages: 103
- Enregistré le: 17 Déc 2007, 20:09
-
 par superkader5 » 10 Mar 2008, 23:55
par superkader5 » 10 Mar 2008, 23:55
merci beaucoup!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
