Continuité uniforme

[mehdi-128]

Bonsoir,

Soit alors :
(1)

Soit . On dit que est uniformément continue si (2)

Je veux montrer que si est uniformément continue alors elle est continue.

Je ne vois pas trop comment faire avec tous ces quantificateurs

[LB2]

Dans la propriété (2), le eta ne dépend pas de x (d'où le nom 'uniforme'), alors que dans la propriété (1), il dépend de x.

On a donc clairement (2) => (1)

En effet, dans (1), (pour tout x) et (pour tout epsilon >0) commutent

[mehdi-128]

Ah merci, je crois avoir compris.

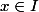
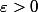
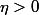
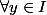
Soit . Soit . D'après (2), il existe un tel que (en effet, est déjà fixé) tel que

D'où le résultat.

[LB2]

Oui (et de plus on peut choisir eta indépendant de x, uniforme en x)