Continuité d'une fonctions à deux variable
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
MoRBT
- Membre Naturel
- Messages: 24
- Enregistré le: 28 Déc 2011, 22:02
-
 par MoRBT » 07 Juin 2012, 17:10
par MoRBT » 07 Juin 2012, 17:10
Boujour,
Je n'arrive pas à calculer la limite à
=(0,0))
de la fonction
= \frac{ x\sin y- y \sin x}{ \textstyle x^2+y^2})
Je voudrais en fait majorer la valeur absolue de
)
mais je ne sais pas comment.
Pourriez-vous m'aider

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 07 Juin 2012, 17:54
par chan79 » 07 Juin 2012, 17:54
MoRBT a écrit:Boujour,
Je n'arrive pas à calculer la limite à
=(0,0))
de la fonction
= \frac{ x\sin y- y \sin x}{ \textstyle x^2+y^2})
Je voudrais en fait majorer la valeur absolue de
)
mais je ne sais pas comment.
Pourriez-vous m'aider
Tu as cherché du côté des développements limités ?
-
MoRBT
- Membre Naturel
- Messages: 24
- Enregistré le: 28 Déc 2011, 22:02
-
 par MoRBT » 07 Juin 2012, 18:55
par MoRBT » 07 Juin 2012, 18:55
chan79 a écrit:Tu as cherché du côté des développements limités ?
Oui j'ai essayé mais je n'ai rien pu faire
-
Dlzlogic
- Membre Transcendant
- Messages: 5273
- Enregistré le: 14 Avr 2009, 12:39
-
 par Dlzlogic » 07 Juin 2012, 20:28
par Dlzlogic » 07 Juin 2012, 20:28
Montrez déjà ce que vous avez écrit.
-
MoRBT
- Membre Naturel
- Messages: 24
- Enregistré le: 28 Déc 2011, 22:02
-
 par MoRBT » 07 Juin 2012, 21:04
par MoRBT » 07 Juin 2012, 21:04
Dlzlogic a écrit:Montrez déjà ce que vous avez écrit.
Je crois que c'est bon:
On a ça:
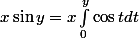
En utilisant l'intégration par partie on aura:
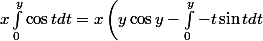=xy\cos y+x\int_0^yt\sin tdt\])
De la même façon, on a:
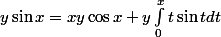
donc:

Et finalement:
|= \frac{|x\sin y-y\sin x|}{x^2+y^2}\leq \frac 12|\cos x-\cos y|+|x|+|y|\])

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 08 Juin 2012, 06:46
par chan79 » 08 Juin 2012, 06:46
MoRBT a écrit:Oui j'ai essayé mais je n'ai rien pu faire
juste une idée à vérifier
la valeur absolue de
-y(x-\fra{x^{3}}{6})}{x^2+y^2})
est majorée par la valeur absolue de xy/6

-
alm
- Membre Relatif
- Messages: 335
- Enregistré le: 15 Jan 2009, 01:00
- Localisation: Salé, Maroc
-
 par alm » 08 Juin 2012, 07:43
par alm » 08 Juin 2012, 07:43
Salut
Si l iégalité est vrais tu as terminé
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités