Continuité d'une fonction
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
pierremaul
- Messages: 8
- Enregistré le: 18 Sep 2006, 18:36
-
 par pierremaul » 03 Déc 2006, 18:20
par pierremaul » 03 Déc 2006, 18:20
Pierre (posté le 28/11/2006 à 20:51) ID: (32629,0)
Bonsoir à tous !
Je bloque depuis plusieurs jours sur la continuité d'une fonction.
En effet, on a vu en cours que:
Soit f une fonction,
f est uniformement continue sur D ( un ensemble ) ==> ( implique) f continue sur D.
On doit montrer que la réciproque fausse en donnant un contre exemple avec : f(x)= ..... et D=.....
Je n'arrive toujours pas à trouver.
Pourriez-vous l'aider svp?
Merci beaucoup et bonne soirée :)

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 03 Déc 2006, 18:46
par nuage » 03 Déc 2006, 18:46
Salut,
tu peux essayer avec
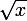
sur [0;1]
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 03 Déc 2006, 19:23
par kazeriahm » 03 Déc 2006, 19:23
nuage le theoreme de Heine ?! :we:
l'exemple de nuage ne marche pas car toute fonction continue sur un segment est uniformement continue sur ce segment.
Parcontre tu peux essayer racine de x sur R (et non pas sur [0,1])
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 03 Déc 2006, 19:34
par abcd22 » 03 Déc 2006, 19:34
Bonsoir,
racine de x est uniformément continue sur R, par contre l'exponentielle par exemple n'est pas uniformément continue sur R. Ou encore sin(1/x) sur ]0,1].
-
pierremaul
- Messages: 8
- Enregistré le: 18 Sep 2006, 18:36
-
 par pierremaul » 03 Déc 2006, 20:43
par pierremaul » 03 Déc 2006, 20:43
Merci pour vos réponses.
Pourriez vous m'expliquer pourquoi sin(1/x) est continu sur ]0,1] mais pas uniformément continue sur ]0,1] ?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 03 Déc 2006, 20:46
par yos » 03 Déc 2006, 20:46
Ou x ---> x² sur R

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 03 Déc 2006, 21:03
par nuage » 03 Déc 2006, 21:03
kazeriahm a écrit:nuage le theoreme de Heine ?! :we:
l'exemple de nuage ne marche pas car toute fonction continue sur un segment est uniformement continue sur ce segment.
Parcontre tu peux essayer racine de x sur R (et non pas sur [0,1])
Mes excuses :briques:
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 03 Déc 2006, 21:34
par abcd22 » 03 Déc 2006, 21:34
pierremaul a écrit:Merci pour vos réponses.
Pourriez vous m'expliquer pourquoi sin(1/x) est continu sur ]0,1] mais pas uniformément continue sur ]0,1] ?
Pour tout entier n, si on pose

et

, on a
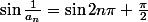} = 1)
et
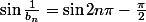} = -1)
. Pour tout
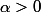
, pour n assez grand

et

, ça contredit la définition de la continuité uniforme pour

.
Intuitivement, la raison pour laquelle cette fonction n'est pas uniformément continue sur ]0 ; 1] c'est qu'elle oscille de plus en plus vite au voisinage de 0.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
