Continuité d'une fonction
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 24 Oct 2006, 19:00
par Babe » 24 Oct 2006, 19:00
Bonjour a tous
Montrez que la fonction definie par:
f(x)=0 si x


et f(x)=1 si x
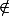

n'est continu en aucun point
Coment dois-je prouver cela ?
merci d'avance
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 24 Oct 2006, 19:20
par tize » 24 Oct 2006, 19:20
Avec la définition de la continuité et aussi avec le fait que dans un intervalle (aussi petit soit il) on peut toujours trouver une infinité de rationnels (et d'irrationnels aussi)
-
drazala
- Membre Naturel
- Messages: 21
- Enregistré le: 23 Oct 2006, 15:24
-
 par drazala » 24 Oct 2006, 19:23
par drazala » 24 Oct 2006, 19:23
Une méthode si tu as vu lacaractérisation séquentielle de la continuité et la caractérisation séquentielle de la densité des rationnels et des irrationnels dans les réels.
Par l'absurde :
Suppose f continue en un point xo.
Comme les rationnels sont denses dans R il existe une suite de rationnels (Un) qui converge vers xo, f étant continue en xo que peux-tu dire de f(xo)?
Même chose les irrationnels etant denses dans R il existe une suite (Vn) d'irrationnels qui convergent vers xo, f étant continue en xo que dire de f(xo)?
Conclusion?
drazala
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 24 Oct 2006, 20:44
par Babe » 24 Oct 2006, 20:44
j'ai compri a peu pres mais pour rediger :mur:
(\exists\alpha>0)\;|x-x_0|<\alpha \Longrightarrow |f(x)-f(x_0)|<\varepsilon)
je suppose qu'il faut partir de la mais après...
edit:rectification
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 24 Oct 2006, 21:07
par tize » 24 Oct 2006, 21:07
Bon une petite aide : ce que tu viens d'écrire est la continuité (avec des erreurs)...c'est :
(\exists\alpha>0)\;|x-x_0|<\alpha \Longrightarrow |f(x)-f(x_0)|<\varepsilon)
Toi tu veux montrer qu'elle n'est pas continue en

quelque soit

. Tu dois donc montrer la négation le la propriété que j'ai écrit ci-dessus...
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 24 Oct 2006, 21:39
par Babe » 24 Oct 2006, 21:39
(\exists\alpha>0)\;|x-x_0|0)(\forall\alpha>0)\;|x-x_0|\varepsilon)
merci de m'aider tize :triste:
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 24 Oct 2006, 21:49
par tize » 24 Oct 2006, 21:49
Oui c'est ça avec un inférieur ou égal ...
(\forall\alpha>0)\;|x-x_0|<\alpha \ et |f(x)-f(x_0)|\geq\varepsilon)
tu peux essayer de montrer cela avec
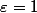
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 25 Nov 2006, 13:42
par Babe » 25 Nov 2006, 13:42
je me permet de faire remonter cet exercice car apparement je m'etais trompé
(\forall\alpha>0)\;|x-x_0|<\alpha \ et |f(x)-f(x_0)|\geq\varepsilon)
avec
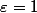
(\forall\alpha>0)\;|x-x_0|<\alpha \ et |f(x)-f(x_0)|\geq\1)
mais je dois continuer comment ?
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 25 Nov 2006, 14:49
par aviateurpilot » 25 Nov 2006, 14:49
soit
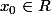
on a
+\pi}{10^n}=x_0 \\ \lim_{n->+\infty}\frac{E(10^nx_0)}{10^n}=x_0) supposont que
supposont que  est continue en
est continue en 
dans ce cas
=\lim_{x->x_0}f(x)=\lim_{n->+\infty}f(\frac{E(10^nx_0)}{10^n})=\lim_{n->+\infty}\ 0=0)
(car
}{10^n}\in Q)
)
et
=\lim_{x->x_0}f(x)=\lim_{n->+\infty}f(\frac{E(10^nx_0)+\pi}{10^n})=\lim_{n->+\infty}\ 1=1)
(car
+\pi}{10^n}\not\in Q)
)
absurddonc

,

n'ai pas continue en

-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 25 Nov 2006, 18:29
par Babe » 25 Nov 2006, 18:29
aurait tu la methode avec la negation de la continuité
(\forall\alpha>0)\;|x-x_0|<\alpha \ et |f(x)-f(x_0)|\geq\varepsilon)
je n'arrive pas a faire la suite
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 25 Nov 2006, 18:50
par tize » 25 Nov 2006, 18:50
Bonsoir,
prends
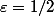
par exemple... pour tout rationnel (resp.irrationnel)

, on peut trouver grâce à la densité des irrationnels (resp. des rationnels) x irrationnel (resp. rationnel) tq pour tout
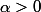
,

et pourtant
-f(x_0)|=1/2)
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 25 Nov 2006, 20:32
par aviateurpilot » 25 Nov 2006, 20:32
aviateurpilot a écrit:soit
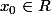
on a
+\pi}{10^n}=x_0 \\ \lim_{n->+\infty}\frac{E(10^nx_0)}{10^n}=x_0) supposont que
supposont que  est continue en
est continue en 
dans ce cas
=\lim_{x->x_0}f(x)=\lim_{n->+\infty}f(\frac{E(10^nx_0)}{10^n})=\lim_{n->+\infty}\ 0=0)
(car
}{10^n}\in Q)
)
et
=\lim_{x->x_0}f(x)=\lim_{n->+\infty}f(\frac{E(10^nx_0)+\pi}{10^n})=\lim_{n->+\infty}\ 1=1)
(car
+\pi}{10^n}\not\in Q)
)
absurddonc

,

n'ai pas continue en

moi je vois que cette methode et plus clair non?
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 25 Nov 2006, 21:03
par Babe » 25 Nov 2006, 21:03
j'ai compris celle de tize mais je n'ai strictement rien compris a la tienne
je suis ouvert a toute explication
PS: le B ce serait pas plutot le E de partie entiere ?
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 25 Nov 2006, 21:12
par aviateurpilot » 25 Nov 2006, 21:12
Babe a écrit:PS: le B ce serait pas plutot le E de partie entiere ?
oui
Babe a écrit:j'ai compris celle de tize mais je n'ai strictement rien compris a la tienne
je suis ouvert a toute explication
tu es en quel niveau scolaire ?
pour que je t'explique par rapport a ton niveau
 par sandrine_guillerme » 25 Nov 2006, 21:15
par sandrine_guillerme » 25 Nov 2006, 21:15
Salut ..
Tiens ce petit
post ça pourrais être assez intèréssant ..
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 25 Nov 2006, 21:24
par Babe » 25 Nov 2006, 21:24
je suis en 1er année de FAC de math-physique
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités