Continuité d'une dérivée partielle
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
srhmrc
- Membre Naturel
- Messages: 52
- Enregistré le: 08 Jan 2024, 13:15
-
 par srhmrc » 23 Déc 2024, 13:30
par srhmrc » 23 Déc 2024, 13:30
Bonjour,
J'ai besoin d'une correction pour un exercice, car je ne suis pas très sûre de mon raisonnement.
L'exercice nous demande si la dérivée partielle en x de
 = \sqrt{x^4+y^4})
est continue à l'origine.
J'ai trouvé que
 = 0)
 = 2x^3(x^4+y^4)^{-1/2})
et donc
 = 2x)
J'ai ensuite calculé
 = 0 = f_x(0,0))
Merci d'avance pour votre aide !
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 23 Déc 2024, 13:49
par GaBuZoMeu » 23 Déc 2024, 13:49
Bonjour,
Pourquoi dis-tu que
=0)
?
Une méthode possible pour étudier la continuité en
)
est de passer en coordonnées polaires.
-
srhmrc
- Membre Naturel
- Messages: 52
- Enregistré le: 08 Jan 2024, 13:15
-
 par srhmrc » 23 Déc 2024, 14:25
par srhmrc » 23 Déc 2024, 14:25
GaBuZoMeu a écrit:Bonjour,
Pourquoi dis-tu que
=0)
?
Une méthode possible pour étudier la continuité en
)
est de passer en coordonnées polaires.
J'ai utilisé
= lim_{h\rightarrow 0 }\frac{f(a+h,b)-f(a,b)}{h})
et j'ai remplacé a,b par 0,0
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 23 Déc 2024, 14:32
par GaBuZoMeu » 23 Déc 2024, 14:32
OK pour la dérivée partielle en (0,0).
As-tu essayé le passage en polaires pour la continuité ? L'argument que tu as donné ne va pas : dans le plan on ne tend pas vers l'origine uniquement suivant l'axe des abscisses !
-
srhmrc
- Membre Naturel
- Messages: 52
- Enregistré le: 08 Jan 2024, 13:15
-
 par srhmrc » 23 Déc 2024, 15:48
par srhmrc » 23 Déc 2024, 15:48
GaBuZoMeu a écrit:OK pour la dérivée partielle en (0,0).
As-tu essayé le passage en polaires pour la continuité ? L'argument que tu as donné ne va pas : dans le plan on ne tend pas vers l'origine uniquement suivant l'axe des abscisses !
En fait, je comprends comment résoudre cet exercice en utilisant une autre méthode (définition de la continuité), mais je ne comprends toujours pas pourquoi mon raisonnement est faux. J'ai du mal à me représenter tout ca en 3D.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 23 Déc 2024, 16:43
par GaBuZoMeu » 23 Déc 2024, 16:43
srhmrc a écrit:J'ai ensuite calculé
 = 0 = f_x(0,0))
Ceci ne donne pas la continuité de
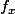
en
)
, mais seulement la continuité de la restriction de
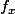
à l'axe des abscisses.
Peux-tu expliquer ce que tu as fait avec ton "autre méthode" ?
-
srhmrc
- Membre Naturel
- Messages: 52
- Enregistré le: 08 Jan 2024, 13:15
-
 par srhmrc » 24 Déc 2024, 17:58
par srhmrc » 24 Déc 2024, 17:58
GaBuZoMeu a écrit: srhmrc a écrit:J'ai ensuite calculé
 = 0 = f_x(0,0))
Ceci ne donne pas la continuité de
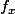
en
)
, mais seulement la continuité de la restriction de
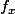
à l'axe des abscisses.
Peux-tu expliquer ce que tu as fait avec ton "autre méthode" ?
Bonjour, j'ai un correctif pour cette méthode, je suis donc sûre que le développement est OK. Merci pour vos réponses, cela m'a été utile !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
?
est de passer en coordonnées polaires.
en
, mais seulement la continuité de la restriction de
à l'axe des abscisses.