Bonjour à tous, je bloque sur un exercice sur la continuité
f:R -> R
x -> E(x) + [x-E(x)]²
Etudier en tout point de R la continuité de f
J'ai essayé de partir de la definition d'une fonction continue et j'ai fait f(x)-f(x0), mais je n'ai pas d'idée pour la suite.
Merci à tous
Continuité
7 messages
- Page 1 sur 1
par skilveg » 24 Jan 2009, 19:14
Essaie de faire un dessin pour voir où ont lieu les éventuels problèmes...
par xyz1975 » 24 Jan 2009, 19:41
Hyperman16 a écrit:Bonjour à tous, je bloque sur un exercice sur la continuité
f:R -> R
x -> E(x) + [x-E(x)]²
Etudier en tout point de R la continuité de f
J'ai essayé de partir de la definition d'une fonction continue et j'ai fait f(x)-f(x0), mais je n'ai pas d'idée pour la suite.
Merci à tous
La fonction f est écrite à partir de la fonction "partie entière", il faut d'abord connaître les propriétés de cette fonction pour pouvoir répondre à cette question.
La partie entière est définie sur IR tout entier, continue en tout point de IR\Z, mais continue à droite en tout point de IR.
Si un problème de continuité se posera pour cette fonction c'est en tout point de Z.
Je peux alors dire que f est continue sur IR\Z comme composée et somme de fonctions elles mêmes continues sur cet ensemble, il suffit d'examiner alors la continuité en tout point de Z uniquement.
par barbu23 » 24 Jan 2009, 19:44
Bonsoir :
Ici, il faut étudier la continuité sur l'intervalle :
avec : 
,ensuite généraliser sur tout :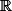 
.
Tu commences comme suit :
Soient : et 
Alors :=n \leq x < E(x)+1=n+1 $)
.
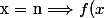 = E(x)-[x-E(x)]^2 =n - (n-n)^2 = 0 $)
 = E(x)-[x-E(x)]^2 = E(x) - x^2 +2.x.E(x)-E(x)^2 = n - x^2 + 2.^n.x - n^2 $)
Donc, Il te suffit maintenant, de verifier la continuité sur l'intervalle ... Je pense que c'est clair maintenant après avoir expliciter la fonction comme çi-dessus .. !
Bonne chance !
Ici, il faut étudier la continuité sur l'intervalle :
Tu commences comme suit :
Soient :
Alors :
Donc, Il te suffit maintenant, de verifier la continuité sur l'intervalle
Bonne chance !
par xyz1975 » 24 Jan 2009, 20:39
J'ai une proposition pour la réponse.
Comme le pb se pose au voisinage de n (entier relatif) je vais étudier la continuité à droite et à gauche en x=n car E(x) prend deux valeurs différentes.
Il est clair que f(n)=E(n)+(n-E(n))²=n+(n-n)²=n et que
Si x tend vers
alors E(x)=n-1.
Si x tend vers
alors E(x)=n.
Par conséquent :
=n-1+(n-(n-1))^2= n=f(n))
f est donc continue à gauche de x=n.
=n+(n-n)^2= n=f(n))
f est donc continue à droite de x=n.
En total f est continue en x=n.
Le but de l'exo est de construire à partir de la fonction E une fonction continue sur IR tout entier.
Comme le pb se pose au voisinage de n (entier relatif) je vais étudier la continuité à droite et à gauche en x=n car E(x) prend deux valeurs différentes.
Il est clair que f(n)=E(n)+(n-E(n))²=n+(n-n)²=n et que
Si x tend vers
Si x tend vers
Par conséquent :
f est donc continue à gauche de x=n.
f est donc continue à droite de x=n.
En total f est continue en x=n.
Le but de l'exo est de construire à partir de la fonction E une fonction continue sur IR tout entier.
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :