Continuité géométrique

[moona]

quels sont les types de continuité dans la modélisation géométriques et quel est le meilleur parmi ces types

merci

[Flodelarab]

La continuité géométrique ou géométrique, était un concept de la géométrie principalement appliqué au sections coniques et formes reliées par des mathématiciens comme Leibnitz , Johannes Kepler , et Poncelet . Le concept était une tentative tôt de décrire, par la géométrie plutôt que l'algèbre, de concept de continuité comme exprimé par a fonction paramétrique . L'idée fondamentale derrière la continuité géométrique était que les cinq sections coniques étaient vraiment cinq versions différentes de la même forme ; il était possible de construire ellipses vers la limite de l'un ou l'autre a cercle ou a parabole , et construire de même hyperbole qui a approché les formes d'a parabole ou un droit ligne . Ainsi, il y avait continuité entre les sections coniques. Ces idées ont mené à d'autres concepts de continuité. Par exemple, si un cercle et une ligne droite étaient deux expressions de la même forme, pourrait une ligne ne pas être considérée comme un cercle de infini rayon ? 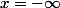Pour que tels soient le cas, on devrait rendre la ligne « continue » en laissant le point x = \infty pour être un point sur le cercle, et pour et pour être identique. De telles idées étaient utiles en ouvrant le moderne, algébriquement défini, idée de continuité d'une fonction et de infini .

[moona]

La continuité géométrique ou géométrique, était un concept de la géométrie principalement appliqué au sections coniques et formes reliées par des mathématiciens comme Leibnitz , Johannes Kepler , et Poncelet . Le concept était une tentative tôt de décrire, par la géométrie plutôt que l'algèbre, de concept de continuité comme exprimé par a fonction paramétrique . L'idée fondamentale derrière la continuité géométrique était que les cinq sections coniques étaient vraiment cinq versions différentes de la même forme ; il était possible de construire ellipses vers la limite de l'un ou l'autre a cercle ou a parabole , et construire de même hyperbole qui a approché les formes d'a parabole ou un droit ligne . Ainsi, il y avait continuité entre les sections coniques. Ces idées ont mené à d'autres concepts de continuité. Par exemple, si un cercle et une ligne droite étaient deux expressions de la même forme, pourrait une ligne ne pas être considérée comme un cercle de infini rayon ? Pour que tels soient le cas, on devrait rendre la ligne « continue » en laissant le point x = \infty pour être un point sur le cercle, et pour et pour être identique. De telles idées étaient utiles en ouvrant le moderne, algébriquement défini, idée de continuité d'une fonction et de infini .

merci Flodelarab pour cette explication,

les courbes de bézier et les splines sont des types de continuité?

[Flodelarab]

Les splines sont la généralisation des courbes de Bézier, elles peuvent être à leur tour généralisées par les NURBS.

[moona]

merci Flodelarab et est ce qu'elles expriment la continuité géométrique?

[Flodelarab]

merci Flodelarab et est ce qu'elles expriment la continuité géométrique?

Ben .... c bizarre comme question.

C'est comme demander si le carré assure la continuité géométrique du rectangle ....
ou si le cercle assure la continuité géométrique de l'ellipse.


Je dirais non car c'est la même chose et oui car c'est la même chose.

[moona]

Ben .... c bizarre comme question.

C'est comme demander si le carré assure la continuité géométrique du rectangle ....
ou si le cercle assure la continuité géométrique de l'ellipse.


Je dirais non car c'est la même chose et oui car c'est la même chose.

je me suis peut être mal exprimé

je parle des courbes en général paramétrique cubique, bézier, b-spline....etc

(c'est la question qui figure dans un exercice et dont la réponse parle de courbes :help: )