Continuité fonction
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
akiwhite
- Membre Naturel
- Messages: 96
- Enregistré le: 22 Sep 2019, 18:36
-
 par akiwhite » 22 Fév 2020, 14:07
par akiwhite » 22 Fév 2020, 14:07
Bonjour,
la question est la suivante : Soient f et g deux fonctions continues sur un intervalle de I de R tel que :
Pour tout
)^{2} = (g(x))^{2} \neq 0)
.
Montrer que l'on a soit f = g soit f = -g.
En fait je me demande s'il on a le droit de suivre le raisonnement suivant :
- f et g sont continues donc f(x)² et g(x)² le sont aussi
-on peut alors simplement appliquer la racine carrée sur ces fonctions puisqu'elles sont positive et en déduire
f = g ou f = -g
Ca me parait trop simple ...
Merci pour vos réponses,
cordialement,
Akiwhite
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 22 Fév 2020, 14:31
par GaBuZoMeu » 22 Fév 2020, 14:31
-
Mimosa
- Membre Relatif
- Messages: 432
- Enregistré le: 19 Aoû 2016, 16:31
-
 par Mimosa » 22 Fév 2020, 14:35
par Mimosa » 22 Fév 2020, 14:35
Bonjour
Ce que tu peux dire, c'est seulement que pour tout

de l'intervalle, tu as
=\pm g(x))
, mais tu ne sais pas si c'est toujours + ou toujours moins.
Si tu prends
=-1)
sur
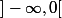
et
=1)
sur

et
=1)
sur
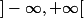
tu as bien
)^2=(g(x))^2)
pour tout

.
Morale: il faut utiliser la continuité!
Désolée, légèrement en retard!
-
akiwhite
- Membre Naturel
- Messages: 96
- Enregistré le: 22 Sep 2019, 18:36
-
 par akiwhite » 22 Fév 2020, 15:36
par akiwhite » 22 Fév 2020, 15:36
Merci pour vos réponses, j'ai compris le soucis.
Mais je ne trouve aucune piste pour le résoudre en utilisant sa continuité ..
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 22 Fév 2020, 15:42
par GaBuZoMeu » 22 Fév 2020, 15:42
On peut penser à considérer la fonction
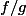
; que peut-on en dire ?
-
LB2
- Habitué(e)
- Messages: 1504
- Enregistré le: 05 Nov 2017, 16:32
-
 par LB2 » 22 Fév 2020, 15:43
par LB2 » 22 Fév 2020, 15:43
Bonjour,
C'est un argument de théorème des valeurs intermédiaires.
La fonction f/g (par exemple) est bien définie, continue, et ses valeurs sont +1 ou -1.
Donc si elle n'est pas constante, par TVI elle passe nécessairement par 0 : contradiction.
Conclusion : f/g est constante, ce qu'on voulait.
@GBZM : oups, désolé
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 22 Fév 2020, 15:45
par GaBuZoMeu » 22 Fév 2020, 15:45
Bravo LB2, tu as fait l'exercice à la place d'akiwhite !
C'est bien, tu as montré que tu savais le faire.
-
akiwhite
- Membre Naturel
- Messages: 96
- Enregistré le: 22 Sep 2019, 18:36
-
 par akiwhite » 22 Fév 2020, 16:00
par akiwhite » 22 Fév 2020, 16:00
Merci à vous !
-
LB2
- Habitué(e)
- Messages: 1504
- Enregistré le: 05 Nov 2017, 16:32
-
 par LB2 » 22 Fév 2020, 16:12
par LB2 » 22 Fév 2020, 16:12
GaBuZoMeu a écrit:Bravo LB2, tu as fait l'exercice à la place d'akiwhite !
C'est bien, tu as montré que tu savais le faire.
Je n'apprécie pas beaucoup ce ton.
J'estime que le questionneur a suffisamment avancé dans sa réflexion pour lui apporter des éléments de solution, et le mot clé "valeurs intermédiaires" n'avait pas encore été donné.
Reste pour lui à comprendre pourquoi l'argument que je donne, qui n'est pas une solution rédigée, fonctionne et s'intègre à sa solution.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 22 Fév 2020, 17:06
par GaBuZoMeu » 22 Fév 2020, 17:06
Et moi je trouve que tu te fiches du monde (et que tu contreviens à la charte du forum).
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
